Wat is recursie?
Wiskundig gezien zijn recursieve functies functies die zichzelf één of meerdere keren oproepen. Een gekend voorbeeld is faculteit: $$ n! = n \times (n-1)! \quad\textrm{met}\quad 0! = 1 $$ Bijvoorbeeld $$\begin{align} 5! & = 5 \times 4! \\ & = 5 \times (4 \times 3!) \\ & = 5 \times (4 \times (3 \times 2!)) \\ & = 5 \times (4 \times (3 \times (2 \times 1!))) \\ & = 5 \times (4 \times (3 \times (2 \times (1 \times 0!)))) \\ & = 5 \times (4 \times (3 \times (2 \times (1 \times 1)))) \\ & = 120 \end{align}$$
Een ander gekend voorbeeld zijn de Fibonacci-getallen \( 0, 1, 1, 2, 3, 5, 8, 13, 21, \ldots \), gegeven door volgende recursieve vergelijking: $$ F(n) = F(n-1) + F(n-2) \quad\textrm{met}\quad F(1) = 1 \quad\textrm{en}\quad F(0) = 0 $$.
In Java kunnen we ook recursieve methodes definiëren. Hier is bijvoorbeeld een recursieve methode om de faculteit van een getal te berekenen:
public static int fac(int n) {
if (n < 0) throw new IllegalArgumentException("n must be non-negative");
if (n == 0) return 1;
return n * fac(n-1);
}
Merk op hoe dicht de implementatie aanleunt bij de wiskundige definitie. Dat geldt ook voor de methode om het n-de Fibonacci-getal te berekenen:
public static int fib(int n) {
if (n < 0) throw new IllegalArgumentException("n must be non-negative");
if (n == 0) return 0;
if (n == 1) return 1;
return fib(n-1) + fib(n-2);
}
Merk op hoe de functie zichzelf tweemaal oproept.
De recursie eindigt wanneer een basisgeval bereikt wordt.
Dat is een situatie (meestal een zeer eenvoudige) waar het antwoord onmiddellijk gekend is, en geen recursieve oproep meer nodig is.
In bovenstaande code voor fib zijn de basisgevallen de oproepen waarin n kleiner is dan 2.
We zouden ook een versie kunnen maken met meer basisgevallen; op zich maakt dat (buiten een klein beetje efficiëntie-winst) weinig verschil.
public static int fib_alt(int n) {
if (n < 0) throw new IllegalArgumentException("n must be non-negative");
if (n == 0) return 0;
if (n == 1) return 1;
if (n == 2) return 1;
if (n == 3) return 2;
if (n == 4) return 3;
if (n == 5) return 5;
return fib_alt(n-1) + fib_alt(n-2);
}
Het belangrijkste bij een recursieve functie is dat de ketting van recursieve oproepen ooit eindigt. Volgende recursieve definitie van Fibonacci zou dus niet goed zijn:
Waarom niet?
public static int fib_bad(int n) {
if (n == 0) return 0;
return fib_bad(n-1) + fib_bad(n-2);
}
Recursie achter de schermen
Wanneer we een recursieve functie uitvoeren, doet Java achter de schermen heel wat boekhouding voor ons.
Bekijk onderstaande illustratie die aangeeft wat er allemaal gebeurt om fib(5)=5 te berekenen:
graph TB
t[" "]
f5["return fib(4) + fib(3)"]
f4["return fib(3) + fib(2)"]
f3["return fib(2) + fib(1)"]
f2_1["return fib(1) + fib(0)"]
f2_2["return fib(1) + fib(0)"]
f1_1["return 1"]
f1_2["return 1"]
f1_3["return 1"]
f0_1["return 0"]
f0_2["return 0"]
f3_2["return fib(2) + fib(1)"]
f2_3["return fib(1) + fib(0)"]
f1_4["return 1"]
f1_5["return 1"]
f0_3["return 0"]
t --> |"fib(5)"| f5
f5 --> |"fib(4)"| f4
f4 -->|"fib(3)"| f3
f3 -->|"fib(2)"| f2_1
f2_1 -->|"fib(1)"| f1_1
f1_1 -->|1| f2_1
f2_1 -->|"fib(0)"| f0_1
f0_1 -->|0| f2_1
f2_1 -->|1| f3
f3 -->|"fib(1)"| f1_2
f1_2 -->|1| f3
f3 -->|2| f4
f4 -->|"fib(2)"| f2_2
f2_2 -->|"fib(1)"| f1_3
f1_3 -->|1| f2_2
f2_2 -->|"fib(0)"| f0_2
f0_2 -->|0| f2_2
f2_2 -->|1| f4
f5 --> |"fib(3)"| f3_2
f3_2 -->|"fib(2)"| f2_3
f2_3 -->|"fib(1)"| f1_4
f1_4 -->|1| f2_3
f2_3 -->|"fib(0)"| f0_3
f0_3 -->|0| f2_3
f2_3 -->|1| f3_2
f3_2 -->|"fib(1)"| f1_5
f1_5 -->|1| f3_2
f3_2 -->|2| f5
f4 -->|3| f5
f5 -->|5| t
classDef base fill:#fcc,stroke:#933
class f0_1,f0_2,f0_3 base
class f1_1,f1_2,f1_3,f1_4,f1_5 base
Stack
De uitvoering van recursieve methodes maakt (net zoals de uitvoering van gewone methodes) gebruik van een stack.
We herschrijven fib lichtjes om de uitleg te vergemakkelijken:
public static int fib(int n) {
if (n < 0) throw new IllegalArgumentException("n must be non-negative");
if (n == 0) return 0;
if (n == 1) return 1;
int fib_n1 = fib(n-1);
int fib_n2 = fib(n-2);
int result = fib_n1 + fib_n2;
return result;
}
Elke methode-oproep voegt een stackframe toe; in dat stackframe worden de waarden van alle parameters (bv. n voor fib hierboven) en lokale variabelen (fib_n1, fib_n2, en result) bewaard.
Het bovenste stackframe is het actieve stackframe.
Wanneer de methode-oproep voltooid is (bijvoorbeeld na het uitvoeren van een return-statement) verdwijnt dat stackframe, en wordt het vorige stackframe terug geactiveerd.
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
classDef active stroke:#363,fill:#afa
class f5 active
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
f5 --> f4
classDef active stroke:#363,fill:#afa
class f4 active
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
**fib_n1=???**
fib_n2=???
result=???`"]
f3["`**fib**
n=3
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
f5 --> f4
f4 --> f3
classDef active stroke:#363,fill:#afa
class f3 active
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
**fib_n1=???**
fib_n2=???
result=???`"]
f3["`**fib**
n=3
fib_n1=1
fib_n2=1
**result=2**`"]
main --> f5
f5 --> f4
f4 --> f3
classDef active stroke:#363,fill:#afa
class f3 active
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
fib_n1=2
**fib_n2=???**
result=???`"]
f3["`**fib**
n=3
fib_n1=1
fib_n2=1
result=2`"]
main --> f5
f5 --> f4
f4 ~~~ f3
classDef active stroke:#363,fill:#afa;
classDef removed stroke:#aaa,fill:#ddd,color:#aaa;
class f4 active
class f3 removed
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
fib_n1=2
**fib_n2=???**
result=???`"]
f2["`**fib**
n=2
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
f5 --> f4
f4 --> f2
classDef active stroke:#363,fill:#afa
class f2 active
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
fib_n1=2
fib_n2=1
**result=3**`"]
main --> f5
f5 --> f4
classDef active stroke:#363,fill:#afa
class f4 active
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f4["`**fib**
n=4
fib_n1=2
fib_n2=1
result=3`"]
f5["`**fib**
n=5
fib_n1=3
**fib_n2=???**
result=???`"]
main --> f5
f5 ~~~ f4
classDef active stroke:#363,fill:#afa
classDef removed stroke:#aaa,fill:#ddd,color:#aaa;
class f5 active
class f4 removed
%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
fib_n1=3
fib_n2=2
**result=5**`"]
main --> f5
classDef active stroke:#363,fill:#afa
class f5 active
Stack overflow
Zoals je hierboven kan zien, groeit de stack bij elke recursieve oproep.
Elke stack-frame neemt een bepaalde hoeveelheid geheugen in.
De totale grootte van de stack is echter beperkt.
Wanneer de stack te groot wordt, krijg je een stack overflow.
In Java uit zich dat door het gooien van een StackOverflowException.
Je kan de grootte die gereserveerd wordt voor de stack vergroten door bij de uitvoering een argument (-Xss) mee te geven aan de Java virtual machine (JVM).
Bijvoorbeeld, om een stack van 4 megabyte te voorzien (de standaardgrootte is gewoonlijk 1 MB):
java -Xss4m Program
In IntelliJ kan je die optie toevoegen in de ‘Run configuration’.
Gewoonlijk zal dat niet nodig zijn; enkel wanneer je gebruik maakt van recursie voor grotere problemen.
Een meer waarschijnlijke oorzaak van een StackOverflowException is een recursieve operatie die niet eindigt in een basisgeval.
Eindigheid en invoergrootte
Indien een recursieve methode niet zorgvuldig gedefinieerd wordt, bestaat de kans dat de recursie nooit stopt, en de methode dus nooit eindigt (tenzij met een StackOverflowException).
Bijvoorbeeld, onderstaande recursieve methode bad
public static int bad(int n) {
if (n == 0) return 0;
return bad(n-2);
}
eindigt enkel voor positieve even getallen (overtuig jezelf hiervan).
Om er zeker van te zijn dat een recursieve methode ooit zal eindigen, moeten we kunnen aantonen dat elke recursieve oproep ooit een basisgeval zal bereiken. Dat is niet altijd eenvoudig of mogelijk. Neem bijvoorbeeld volgende welgekende functie van Collatz, gedefinieerd voor \( n \geq 1 \):
public static boolean collatz(int n) {
if (n == 1) {
return true;
} else if (n % 2 == 0) { // n is even
return collatz(n / 2);
} else { // n is oneven > 1
return collatz(3*n + 1);
}
}
Wanneer we die uitvoeren voor n=5 krijgen we als waarden voor n achtereenvolgens 5, 16, 8, 4, 2, 1 en eindigt de recursie dus na 6 oproepen.
Voor n=12 krijgen we 12, 6, 3, 10, 5, 16, 8, 4, 2, 1, en voor n=19 krijgen we 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1.
De reeks waarden in deze voorbeelden lijkt dus steeds te eindigen op n=1, maar is dit zo voor elke beginwaarde van n?
Er zijn geen gekende tegenvoorbeelden, maar er is ook geen bewijs dat dit het geval is voor elke beginwaarde van n.
Bewijzen dat een recursieve functie eindigt is echter wel vanzelfsprekend als elke recursieve oproep de grootte van de invoer strikt kleiner maakt, en de basisgevallen overeenkomen met de kleinst mogelijke invoergrootte(s). Aangezien een invoergrootte steeds (per definitie) een niet-negatief getal moet zijn, moet een voortdurende verkleining ervan ooit stoppen.
Typische invoergroottes bij recursieve problemen zijn
- de waarde van een parameter, indien dit een natuurlijk getal is (bijvoorbeeld
ninfibhierboven) - het aantal elementen in een datastructuur (lijst, set, …) die gebruikt wordt.
Maakt de collatz-methode de invoer steeds strikt kleiner?
Recursief denken
Recursie biedt vaak een erg krachtige manier om complexe algoritmische problemen op te lossen. Je moet hiervoor wel op de juiste manier redeneren over recursie. Een grote valkuil is nadenken over de volledige uitvoeringsboom, zoals we hierboven getoond hebben voor de Fibonacci-functie. De complexiteit hiervan is gigantisch, en staat een elegante oplossing en helder redeneren in de weg.
Een betere manier om na te denken over recursie gaat als volgt. Je wil een probleem van een bepaalde grootte \( n \) oplossen. Stel nu dat je mag veronderstellen dat je (magischerwijze) datzelfde probleem al kan oplossen, maar dan alleen voor alle (strikt kleinere) groottes \( n’ < n \). Hoe kan dit je helpen om het volledige probleem op te lossen? Met andere woorden, welke manieren zie je om een oplossing van een deel van het probleem te transformeren in een oplossing voor het hele probleem? Of nog anders gezegd: recursie gaat om vertrouwen: vertrouw erop dat het kleinere probleem juist opgelost wordt, en besteed enkel aandacht aan hoe je de oplossing voor een kleiner probleem kan gebruiken om de oplossing voor het grotere probleem te vinden. Eens je deze denkwijze onder de knie hebt, wordt recursie bijna een magisch stuk gereedschap.
We bekijken twee voorbeelden van deze denkwijze.
Voorbeeld 1: grootste element
Veronderstel dat je het grootste element uit een lijst van getallen wil bepalen (vergeet even dat we dat ook makkelijk kunnen met behulp van een lus). We noemen de lengte van die lijst \( n \). Stel nu dat we reeds beschikken over een magische oplossing (een functie) om het grootste element te vinden in alle lijsten met een lengte tot en met \( n-1 \). Hoe kunnen we deze oplossing gebruiken om het probleem op te lossen voor een lijst van lengte \( n \)?
Denk hier even zelf over na!
Er zijn verschillende mogelijkheden. We weten bijvoorbeeld dat het grootste element ofwel het eerste element is, ofwel voorkomt in de rest van de lijst (alle elementen behalve het eerste). We kunnen onze magische functie dus gebruiken om het grootste element uit de rest van de lijst te zoeken, en dat vervolgens te vergelijken met het eerste. Dat leidt tot volgende recursieve implementatie:
public static int largestElement(List<Integer> list) {
if (list.isEmpty()) throw new NoSuchElementException();
if (list.size() == 1) return list.getFirst();
var firstElement = list.getFirst();
var largestRest = largestElement(list.subList(1, list.size()));
return Math.max(firstElement, largestRest);
}
De basisgevallen hier zijn een lege lijst (er is dan geen grootste element) en een lijst met slechts één element (dat ene element moet het grootste element zijn).
Merk op hoe we een subList gebruiken om makkelijk een kleinere lijst (zonder het element op index 0) te creëren voor de recursieve oproep.
Zoals je je misschien herinnert, is het resultaat van subList een view op de originele lijst — er worden geen elementen gekopieerd.
Dat is dus zeer efficiënt.
Er waren ook andere oplossingsstrategieën mogelijk met een gelijkaardige denkwijze. Bijvoorbeeld, we hadden het laatste element kunnen afzonderen in plaats van het eerste. Of we hadden het maximum van de eerste helft van de elementen kunnen vergelijken met het maximum van de tweede helft:
public static int largestElement_alt(List<Integer> list) {
if (list.isEmpty()) throw new NoSuchElementException();
if (list.size() == 1) return list.getFirst();
int n = list.size();
var largestFirstHalf = largestElement(list.subList(0, n/2));
var largestSecondHalf = largestElement(list.subList(n/2, n));
return Math.max(largestFirstHalf, largestSecondHalf);
}
Recursief denken lijkt voor dit voorbeeld misschien wat overbodig. Het maximum zoeken kan je inderdaad ook heel eenvoudig iteratief (met een for-lus). Daarom volgt een tweede voorbeeld, waar een iteratieve oplossing niet voor de hand ligt.
Voorbeeld 2: Toren van Hanoi
Je kent misschien de puzzel van de toren van Hanoi. We hebben drie stapels (A, B, en C), en op elke stapel mogen schijven liggen, van groot (onderaan) naar klein (bovenaan). De puzzel bestaat eruit om alle schijven van één stapel naar een andere te verplaatsen. Daarbij zijn er twee regels:
- Je mag slechts 1 schijf per keer verplaatsen.
- Een schijf mag nooit op een kleinere schijf terecht komen.

Hoe moeilijk/lang verwacht je dat een algoritme wordt om deze puzzel op te lossen?
Dit probleem wordt heel eenvoudig als we recursief denken. We moeten \( n \) schijven verplaatsen van een bronstapel (bijvoorbeeld A) naar een doelstapel (bijvoorbeeld C), en we hebben een extra stapel (B) die we als hulpstapel kunnen gebruiken. We vertrouwen er bovendien op dat we een magische oplossing (recursie!) hebben om \( n-1 \) (of minder) schijven te verplaatsen van een willekeurige stapel naar een andere willekeurige stapel, volgens de regels van de puzzel. Hoe kunnen we die magische oplossing gebruiken om het hele probleem op te lossen?
Denk hier zelf even over na!
We kunnen eerst de bovenste \( n-1 \) schijven verplaatsen van stapel A naar stapel B (de hulpstapel). De laatste overblijvende schijf op stapel A (de grootste schijf) verplaatsen we nu naar doelstapel C. Tenslotte verplaatsen we de \( n-1\) schijven van hulpstapel B ook naar doelstapel C (opnieuw via onze magische oplossing). Het basisgeval is heel eenvoudig: indien we 0 schijven moeten verplaatsen, doen we niets.
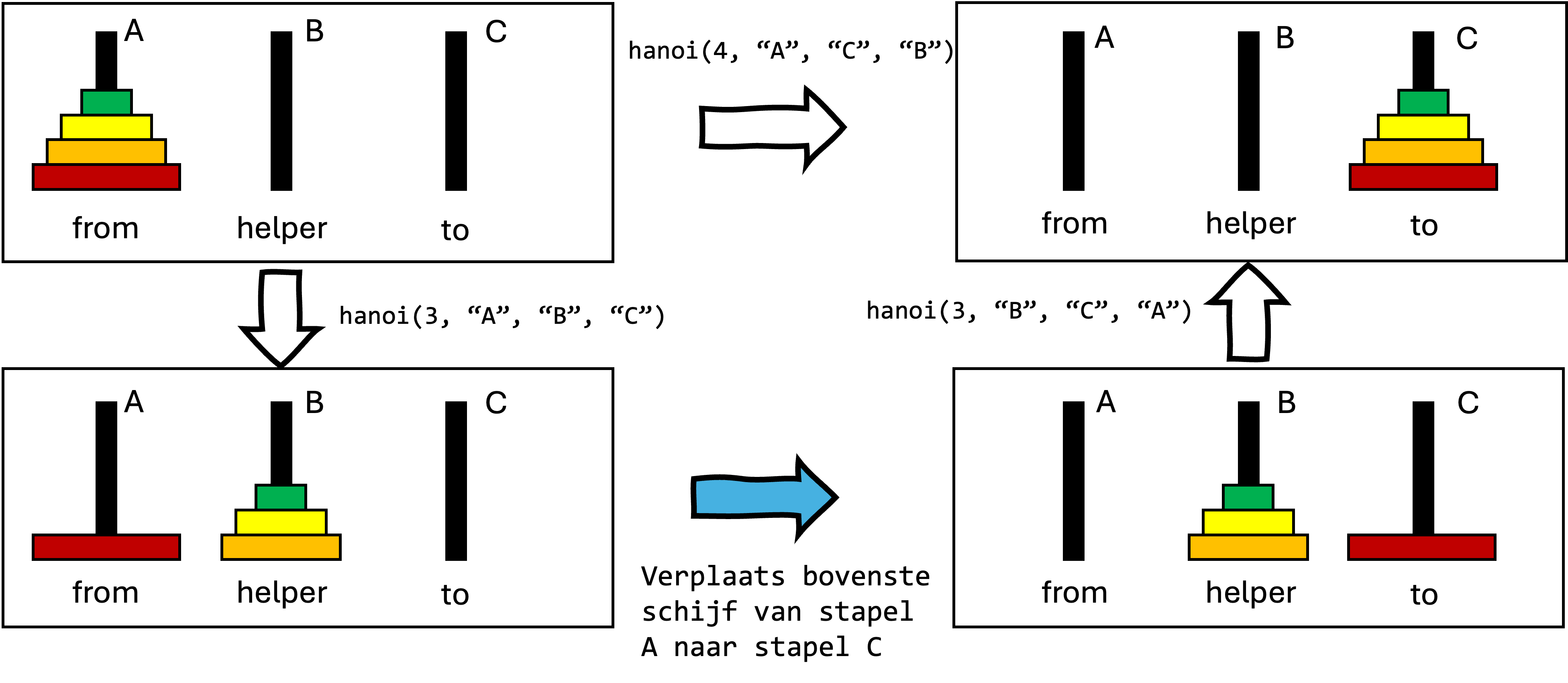
Dat geeft volgende oplossing in code, met n het aantal schijven en from, to, en helper de namen van de stapels, (bijvoorbeeld “A”, “B”, en “C”, of “links”, “midden”, en “rechts”):
public static void hanoi(int n, String from, String to, String helper) {
if (n <= 0) return;
hanoi(n-1, from, helper, to); // verplaats n-1 schijven van `from` naar `helper`, met `to` als hulpstapel
System.out.println("Verplaats de bovenste schijf van stapel " + from + " naar stapel " + to);
hanoi(n-1, helper, to, from); // verplaats n-1 schijven van `helper` naar `to`, met `from` als hulpstapel
}
Erg kort en elegant, niet?
Als we deze oplossing uitvoeren voor n=4 en from="A", to="C", en helper="B", krijgen we volgende uitvoer:
Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel C
Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel C naar stapel A
Verplaats de bovenste schijf van stapel C naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel A
Verplaats de bovenste schijf van stapel C naar stapel A
Verplaats de bovenste schijf van stapel B naar stapel C
Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel C
Ga na dat dit een correcte oplossing is voor het probleem, bijvoorbeeld via deze simulator.
Ter illustratie: de volledige uitvoeringsboom die bij bovenstaande uitvoer hoort ziet er als volgt uit; je leest de oplossing van boven naar onder af in de groene nodes. Het spreekt hopelijk voor zich dat denken over recursie in termen van zo’n bijhorende uitvoeringsboom niet de makkelijkste of duidelijkste manier is.
graph LR
H4ACB["1: hanoi(4,A,C,B)"]
H4ACBH3ABC["2: hanoi(3,A,B,C)"]
H4ACBH3ABCH2ACB["3: hanoi(2,A,C,B)"]
H4ACBH3ABCH2ACBH1ABC["4: hanoi(1,A,B,C)"]
H4ACBH3ABCH2ACBH1ABCH0ACB["5: hanoi(0,A,C,B)"]
H4ACBH3ABCH2ACBH1ABC --> H4ACBH3ABCH2ACBH1ABCH0ACB
H4ACBH3ABCH2ACBH1ABC --> H4ACBH3ABCH2ACBH1ABCm["6: Move A to B"]:::move
H4ACBH3ABCH2ACBH1ABCH0CBA["7: hanoi(0,C,B,A)"]
H4ACBH3ABCH2ACBH1ABC --> H4ACBH3ABCH2ACBH1ABCH0CBA
H4ACBH3ABCH2ACB --> H4ACBH3ABCH2ACBH1ABC
H4ACBH3ABCH2ACB --> H4ACBH3ABCH2ACBm["8: Move A to C"]:::move
H4ACBH3ABCH2ACBH1BCA["9: hanoi(1,B,C,A)"]
H4ACBH3ABCH2ACBH1BCAH0BAC["10: hanoi(0,B,A,C)"]
H4ACBH3ABCH2ACBH1BCA --> H4ACBH3ABCH2ACBH1BCAH0BAC
H4ACBH3ABCH2ACBH1BCA --> H4ACBH3ABCH2ACBH1BCAm["11: Move B to C"]:::move
H4ACBH3ABCH2ACBH1BCAH0ACB["12: hanoi(0,A,C,B)"]
H4ACBH3ABCH2ACBH1BCA --> H4ACBH3ABCH2ACBH1BCAH0ACB
H4ACBH3ABCH2ACB --> H4ACBH3ABCH2ACBH1BCA
H4ACBH3ABC --> H4ACBH3ABCH2ACB
H4ACBH3ABC --> H4ACBH3ABCm["13: Move A to B"]:::move
H4ACBH3ABCH2CBA["14: hanoi(2,C,B,A)"]
H4ACBH3ABCH2CBAH1CAB["15: hanoi(1,C,A,B)"]
H4ACBH3ABCH2CBAH1CABH0CBA["16: hanoi(0,C,B,A)"]
H4ACBH3ABCH2CBAH1CAB --> H4ACBH3ABCH2CBAH1CABH0CBA
H4ACBH3ABCH2CBAH1CAB --> H4ACBH3ABCH2CBAH1CABm["17: Move C to A"]:::move
H4ACBH3ABCH2CBAH1CABH0BAC["18: hanoi(0,B,A,C)"]
H4ACBH3ABCH2CBAH1CAB --> H4ACBH3ABCH2CBAH1CABH0BAC
H4ACBH3ABCH2CBA --> H4ACBH3ABCH2CBAH1CAB
H4ACBH3ABCH2CBA --> H4ACBH3ABCH2CBAm["19: Move C to B"]:::move
H4ACBH3ABCH2CBAH1ABC["20: hanoi(1,A,B,C)"]
H4ACBH3ABCH2CBAH1ABCH0ACB["21: hanoi(0,A,C,B)"]
H4ACBH3ABCH2CBAH1ABC --> H4ACBH3ABCH2CBAH1ABCH0ACB
H4ACBH3ABCH2CBAH1ABC --> H4ACBH3ABCH2CBAH1ABCm["22: Move A to B"]:::move
H4ACBH3ABCH2CBAH1ABCH0CBA["23: hanoi(0,C,B,A)"]
H4ACBH3ABCH2CBAH1ABC --> H4ACBH3ABCH2CBAH1ABCH0CBA
H4ACBH3ABCH2CBA --> H4ACBH3ABCH2CBAH1ABC
H4ACBH3ABC --> H4ACBH3ABCH2CBA
H4ACB --> H4ACBH3ABC
H4ACB --> H4ACBm["24: Move A to C"]:::move
H4ACBH3BCA["25: hanoi(3,B,C,A)"]
H4ACBH3BCAH2BAC["26: hanoi(2,B,A,C)"]
H4ACBH3BCAH2BACH1BCA["27: hanoi(1,B,C,A)"]
H4ACBH3BCAH2BACH1BCAH0BAC["28: hanoi(0,B,A,C)"]
H4ACBH3BCAH2BACH1BCA --> H4ACBH3BCAH2BACH1BCAH0BAC
H4ACBH3BCAH2BACH1BCA --> H4ACBH3BCAH2BACH1BCAm["29: Move B to C"]:::move
H4ACBH3BCAH2BACH1BCAH0ACB["30: hanoi(0,A,C,B)"]
H4ACBH3BCAH2BACH1BCA --> H4ACBH3BCAH2BACH1BCAH0ACB
H4ACBH3BCAH2BAC --> H4ACBH3BCAH2BACH1BCA
H4ACBH3BCAH2BAC --> H4ACBH3BCAH2BACm["31: Move B to A"]:::move
H4ACBH3BCAH2BACH1CAB["32: hanoi(1,C,A,B)"]
H4ACBH3BCAH2BACH1CABH0CBA["33: hanoi(0,C,B,A)"]
H4ACBH3BCAH2BACH1CAB --> H4ACBH3BCAH2BACH1CABH0CBA
H4ACBH3BCAH2BACH1CAB --> H4ACBH3BCAH2BACH1CABm["34: Move C to A"]:::move
H4ACBH3BCAH2BACH1CABH0BAC["35: hanoi(0,B,A,C)"]
H4ACBH3BCAH2BACH1CAB --> H4ACBH3BCAH2BACH1CABH0BAC
H4ACBH3BCAH2BAC --> H4ACBH3BCAH2BACH1CAB
H4ACBH3BCA --> H4ACBH3BCAH2BAC
H4ACBH3BCA --> H4ACBH3BCAm["36: Move B to C"]:::move
H4ACBH3BCAH2ACB["37: hanoi(2,A,C,B)"]
H4ACBH3BCAH2ACBH1ABC["38: hanoi(1,A,B,C)"]
H4ACBH3BCAH2ACBH1ABCH0ACB["39: hanoi(0,A,C,B)"]
H4ACBH3BCAH2ACBH1ABC --> H4ACBH3BCAH2ACBH1ABCH0ACB
H4ACBH3BCAH2ACBH1ABC --> H4ACBH3BCAH2ACBH1ABCm["40: Move A to B"]:::move
H4ACBH3BCAH2ACBH1ABCH0CBA["41: hanoi(0,C,B,A)"]
H4ACBH3BCAH2ACBH1ABC --> H4ACBH3BCAH2ACBH1ABCH0CBA
H4ACBH3BCAH2ACB --> H4ACBH3BCAH2ACBH1ABC
H4ACBH3BCAH2ACB --> H4ACBH3BCAH2ACBm["42: Move A to C"]:::move
H4ACBH3BCAH2ACBH1BCA["43: hanoi(1,B,C,A)"]
H4ACBH3BCAH2ACBH1BCAH0BAC["44: hanoi(0,B,A,C)"]
H4ACBH3BCAH2ACBH1BCA --> H4ACBH3BCAH2ACBH1BCAH0BAC
H4ACBH3BCAH2ACBH1BCA --> H4ACBH3BCAH2ACBH1BCAm["45: Move B to C"]:::move
H4ACBH3BCAH2ACBH1BCAH0ACB["46: hanoi(0,A,C,B)"]
H4ACBH3BCAH2ACBH1BCA --> H4ACBH3BCAH2ACBH1BCAH0ACB
H4ACBH3BCAH2ACB --> H4ACBH3BCAH2ACBH1BCA
H4ACBH3BCA --> H4ACBH3BCAH2ACB
H4ACB --> H4ACBH3BCA
classDef move stroke:green,fill:#afa
Recursie vs. iteratie
In sommige gevallen kan je een for- of while-lus eenvoudig herschrijven tot een recursieve methode en omgekeerd. Die omzetting volgt vaak eenzelfde patroon. Gegeven volgende while- of for-lus (in pseudocode):
R solve(input) {
initialize result
initialize helpers
while (!finished) {
update result and helpers
}
return result
}
R solve(input) {
initialize result
for (initialize helpers; !finished; update helpers) {
update result
}
return result
}
kunnen we volgende equivalente recursieve versie schrijven (opnieuw in pseudo-code):
R solve(input) {
return solve_worker(input, initialResult, initialHelpers);
}
R solve_worker(input, result, helpers) {
if (finished) return result;
update result and helpers
return solve_worker((smaller) input, result, helpers);
}
Bijvoorbeeld, de iteratieve versie om faculteit te berekenen met een for-lus ziet er als volgt uit:
public int factorial(int n) {
if (n < 0) throw new IllegalArgumentException("n must be positive");
int result = 1;
for (int x = n; x > 0; x--) {
result *= x;
}
return result;
}
En de bijhorende recursieve versie (volgens bovenstaand schema):
public int factorial(int n) {
if (n < 0) throw new IllegalArgumentException("n must be positive");
return factorial_worker(n, 1);
}
private int factorial_worker(int x, int result) {
if (x <= 0) return result;
result *= x;
x--;
return factorial_worker(x, result);
}
De factorial_worker methode kunnen we ook nog wat korter schrijven:
public int factorial(int n) {
if (n < 0) throw new IllegalArgumentException("n must be positive");
return factorial_worker(n, 1);
}
private int factorial_worker(int n, int result) {
if (n == 0) return result;
return factorial_worker(n - 1, n * result);
}
Deze recursieve oplossing bestaat uit 2 methodes; je herinnert je misschien nog dat de fac-methode aan het begin van deze pagina uit slechts 1 recursieve methode bestond:
public static int fac(int n) {
if (n < 0) throw new IllegalArgumentException("n must be non-negative");
if (n == 0) return 1;
return n * fac(n-1);
}
Het verschil is dat we bij factorial gebruik maakten van het worker-wrapper patroon voor recursie.
Dat patroon zie je vaak opduiken.
De recursieve factorial_worker-methode (met 2 parameters) is de worker (daar gebeurt het eigenlijke werk), en de (niet-recursieve) factorial-methode met 1 parameter is de wrapper (die roept enkel de worker op met beginwaarden voor de extra parameters).
Hulpvariabelen (hier het voorlopige resultaat, namelijk result) worden doorgegeven als parameters van de worker-methode.
Die parameter wordt ook vaak de ‘accumulator’ genoemd, aangezien die het resultaat bijhoudt van al het werk dat tot dan toe gebeurd is.
De factorial_worker-methode is ook tail-recursive.
Dat betekent dat de recursieve oproep de laatste bewerking is die gebeurt voor de functie eindigt (ze staat direct achter de ‘return’).
In sommige programmeertalen (maar niet in Java) worden dergelijke tail-recursive oproepen geoptimaliseerd door de compiler: aangezien er geen werk meer uitgevoerd moet worden na de recursieve oproep, kan het stackframe meteen ook verwijderd worden. Je loopt dan geen risico op een stack overflow door teveel recursieve oproepen.
Efficiëntie
Wie goed kijkt naar de uitvoeringsboom van fib(5) hierboven kan zien dat er delen van de boom zijn die terugkeren.
Bijvoorbeeld, fib(3) wordt tweemaal opnieuw berekend, fib(2) driemaal, en fib(1) komt vijfmaal voor.
Dat is natuurlijk niet erg efficiënt.
Technieken zoals ‘dynamisch programmeren’ (dynamic programming) en memoization kunnen hier soelaas bieden. We gebruiken deze technieken niet verder binnen deze cursus, maar illustreren hier kort even het achterliggende idee.
Een voorbeeld van hoe memoization gebruikt kan worden voor Fibonacci gaat als volgt (merk op dat we ook het worker-wrapper patroon gebruiken):
public static int fib(int n) {
if (n < 0) throw new IllegalArgumentException();
int[] memo = new int[n+1];
Arrays.fill(memo, -1);
return fib_memoized(n, memo);
}
private static int fib_memoized(int n, int[] memo) {
var result = memo[n];
if (result == -1) {
if (n == 0) result = 0;
else if (n == 1) result = 1;
else result = fib_memoized(n-1, memo) + fib_memoized(n-2, memo);
memo[n] = result;
}
return result;
}
We maken gebruik van een array memo.
Initieel zijn alle elementen daarvan gelijk aan -1, wat hier betekent dat ze nog niet berekend zijn.
Telkens het n-de Fibonacci-getal berekend wordt, slaan we het op op plaats memo[n].
Wanneer dit getal later opnieuw opgevraagd wordt, berekenen we het niet opnieuw, maar herbruiken we gewoon het resultaat van de vorige keer.
Voor \( n=20 \) gebeuren er in de gewone implementatie 6765 oproepen van de fib-methode.
De versie met memoization doet in totaal 39 oproepen van fib_memoized; alle andere oproepen werden vervangen door het uitlezen van het resultaat uit de memo-array.
Je kan dit nog verder optimaliseren: je weet dat elke oproep alleen de vorige twee waarden nodig heeft: om het n-de fibonacci-getal te berekenen heb je enkel het (n-1)‘ste en (n-2)‘de fibonacci-getal nodig. Je hoeft dus niet alle waarden bij te houden in een array, enkel de laatste twee (dat kan met twee variabelen). En in plaats van te vertrekken bij het n-de Fibonacci-getal en naar kleinere Fibonacci-getallen te gaan, kunnen we ook beginnen bij de kleinste Fibonacci-getallen en omhoog gaan tot we uiteindelijk bij het n-de uitkomen.
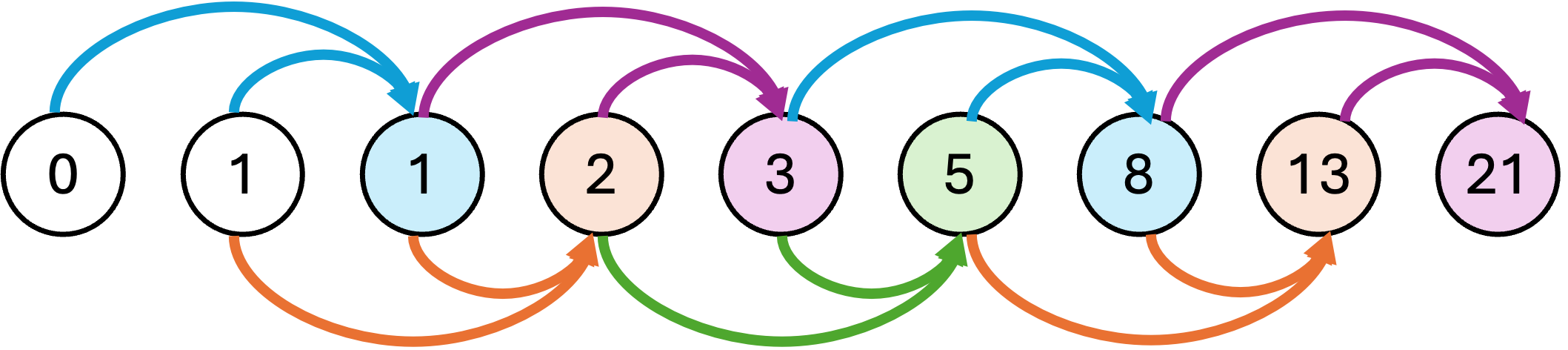
Dat leidt tot volgende recursieve oplossing (opnieuw met het worker-wrapper patroon), waar prevprev en prev de vorige twee waarden voorstellen.
public static int fib(int n) {
if (n < 0) throw new IllegalArgumentException();
if (n == 0) return 0;
if (n == 1) return 1;
return fib_worker(n, 2, 0, 1); // n >= 2
}
private static int fib_worker(int targetN, int currentN, int prevprev, int prev) {
if (currentN == targetN) return prevprev + prev; // fib(n-2) + fib(n-1)
return fib_worker(targetN, currentN+1, prev, prevprev+prev);
}
Hieronder zie je de oproepen van fib_worker om fib(6) te berekenen.
| targetN | currentN | prevprev | prev | returns |
|---|---|---|---|---|
| 6 | 2 | 0 | 1 | fib_worker(6, 3, 1, 0+1=1) |
| 6 | 3 | 1 | 1 | fib_worker(6, 4, 1, 1+1=2) |
| 6 | 4 | 1 | 2 | fib_worker(6, 5, 2, 1+2=3) |
| 6 | 5 | 2 | 3 | fib_worker(6, 6, 3, 2+3=5) |
| 6 | 6 | 3 | 5 | 3 + 5 = 8 |
Deze versie kan ook makkelijk iteratief geschreven worden:
public static int fib(int n) {
if (n < 0) throw new IllegalArgumentException();
if (n == 0) return 0;
if (n == 1) return 1;
int prevprev = 0;
int prev = 1;
for (int x = 2; x != n; x++) {
int newprevprev = prev;
int newprev = prevprev + prev;
prevprev = newprevprev;
prev = newprev;
}
return prevprev + prev;
}
Onderzoek de gelijkenissen en verschillen tussen de recursieve en iteratieve versie.
Oefeningen
Je vind tests en skelet-code voor de oefeningen op Github, in de folder ‘recursie’.
Palindroom
Schrijf een recursieve functie isPalindrome die nagaat of een String een palindroom is.
Een String is een palindroom als die hetzelfde is van links naar rechts als van rechts naar links, bijvoorbeeld
racecarleveldeifiedlepeldroomoordreddermeetsysteemkoortsmeetsysteemstrook
String omkeren
Schrijf een recursieve methode reverse om een String om te keren, bijvoorbeeld:
Hello->olleHracecar->racecar
Element zoeken in lijst
Schrijf een recursieve functie <T> int search(List<T> list, T element) die nagaat of het gegeven element voorkomt in de gegeven lijst.
Als het element voorkomt, wordt de index teruggegeven, anders -1.
- Maak eerst een versie die werkt voor een willekeurige (niet-gesorteerde) lijst.
- Maar vervolgens een snellere versie die werkt voor een gesorteerde lijst, door het te doorzoeken stuk van de lijst telkens halveert en slechts in één van die helften verder gaat zoeken. (Dit is ‘binary search’)
Duplicaten verwijderen
Schrijf een recursieve methode removeDuplicateCharacters die opeenvolgende dezelfde karakters uit een String verwijdert.
Bijvoorbeeld:
aaaaa->akoortsmeetsysteemstrook->kortsmetsystemstrokAAAbbCdddAAA->AbCdA
Greatest common divisor
Schrijf een functie gcd die de grootste gemene deler bepaalt tussen twee getallen.
Maak gebruik van het feit dat, als \( x \geq y \), dat dan \( \gcd(x, y) = \gcd(y, x \% y) \) met % de modulo-operatie, en dat \( \gcd(x, 0) = x \).
Snelle macht
Schrijf een recursieve functie double power(double x, int n) die \( x^n \) berekent met zo weinig mogelijk berekeningen.
Maak gebruik van het feit dat \( x^{2n} = x^n \cdot x^n \) en \( x^{2n+1} = x \cdot x^{2n} \).
Sum of digits
Schrijf een recursieve methode int sumOfDigits(long number) die de som van de cijfers van een (niet-negatief) getal berekent, en dat herhaalt tot die som kleiner is dan 10.
Bijvoorbeeld: 62984 geeft 6+2+9+8+4 = 29; dat wordt vervolgens 2+9 = 11; en dat wordt uiteindelijk 1+1 = 2.
Het resultaat is dus 2.
Trap beklimmen
Schrijf een functie om te berekenen hoeveel verschillende manieren er zijn om een trap met \( n \) treden op te gaan, als je bij elke stap kan kiezen om 1 of 2 treden tegelijk te nemen. Bijvoorbeeld, een trap met \( n = 4 \) treden kan je op 5 verschillende manieren beklimmen:
- 1 trede, 1 trede, 1 trede, 1 trede
- 1 trede, 1 trede, 2 treden
- 1 trede, 2 treden, 1 trede
- 2 treden, 1 trede, 1 trede
- 2 treden, 2 treden
Gepast betalen
Schrijf een recursieve methode boolean kanGepastBetalen(int bedrag, List<Integer> munten) die nagaat of je het gegeven bedrag (uitgedrukt in eurocent) gepast kan betalen met (een deel van) de gegeven munten (en briefjes).
Bijvoorbeeld:
kanGepastBetalen(20, List.of(50, 10, 10, 5))geeft true terug, want 10+10 = 20.kanGepastBetalen(125, List.of(100, 100, 50, 20, 10, 5 ))geeft true terug, want 100+20+5 = 125.kanGepastBetalen(260, List.of(100, 100, 50, 20, 5 ))geeft false terug: er is geen combinatie van munten die samen 260 geeft.
Gepast betalen (bis)
Gegeven een lijst van muntwaarden (bv. 5, 10, 20, 50, 100, 200), schrijf een recursieve methode int countChange(int amount, List<Integer> coinValues) die bepaal op hoeveel manieren je een specifiek bedrag kan betalen.
Je mag nu veronderstellen dat je een voldoende aantal (of oneindig veel) munten van elke opgegeven waarde hebt.
Bijvoorbeeld, met bovenstaande muntwaarden
- kan je een bedrag van 35 betalen op 6 manieren:
- 7×5
- 1×10 en 5×5
- 1×10 en 1×20 en 1×5
- 2×10 en 3×5
- 3×10 en 1×5
- 1×20 en 3×5
- kan je een bedrag van 260 betalen op 646 manieren
- kan je een bedrag van 1000 betalen op 98411 manieren
Alle prefixen van een String
Schrijf een recursieve functie allPrefixes die een Set teruggeeft met alle prefixen van een gegeven String.
Bijvoorbeeld:
allPrefixes("cat") == { "", "c", "ca", "cat" }allPrefixes("Hello") == { "", "H", "He", "Hel", "Hell", "Hello" }
Alle interleavings van twee strings
Schrijf een recursieve functie allInterleavings(String s1, String s2) die een Set teruggeeft met alle interleavings van de twee strings s1 en s2.
Een interleaving is een nieuwe string met daarin alle karakters van de eerste en de tweede string, in dezelfde volgorde waarin ze in elk van de originele strings voorkomen, maar mogelijk door elkaar.
Bijvoorbeeld:
allInterleavings("A", "B") = [AB, BA]allInterleavings("ABC", "x") = [ABCx, ABxC, AxBC, xABC]allInterleavings("AB", "xy") = [ABxy, AxBy, AxyB, xABy, xAyB, xyAB]allInterleavings("ABC", "xy") = [ABCxy, ABxCy, ABxyC, AxBCy, AxByC, AxyBC, xABCy, xAByC, xAyBC, xyABC]
Vliegtuigreis
Gegeven een record Item:
record Item(String name, int weight) {}
schrijf een methode List<Item> pack(List<Item> choices, int maxWeight) die een keuze maakt uit de gegeven lijst van items, zodanig dat je zoveel mogelijk items kan meenemen zonder dat het totale gewicht hoger wordt dan het maximumgewicht (opgelegd door de vliegtuigmaatschappij).
Bijvoorbeeld, met 3 items (A: 50, B: 20, C: 10, en D: 5):
- met een totaal toegelaten gewicht van 100 kan je alle items meenemen;
- met een totaal toegelaten gewicht van 40 kan je maximaal 3 items meenemen (B, C, en D);
- met een totaal toegelaten gewicht van 20 kan je maximaal 2 items meenemen (C en D);
Powerset
Schrijf een recursieve functie Set<Set<T>> powerset(Set<T> s) die de powerset berekent van de gegeven set s.
De powerset is de set van alle deelverzamelingen van s.
Bijvoorbeeld:
powerset(Set.of("A", "B")) = [[], [A], [B], [A, B]]powerset(Set.of("A", "B", "C")) = [[], [A], [B], [C], [A, B], [A, C], [B, C], [A, B, C]]
Alle permutaties van een lijst berekenen
Schrijf een functie allPermutations die een Set teruggeeft met alle permutaties van een gegeven lijst.
Bijvoorbeeld:
allPermutations(List.of("A", "B")) = [ [A, B], [B, A] ]allPermutations(List.of("A", "B", "C")) = [ [A, B, C], [A, C, B], [B, A, C], [B, C, A], [C, A, B], [C, B, A] ]
Gebalanceerde haakjes
Schrijf een recursieve methode boolean balancedParentheses(String s) die nagaat of alle haakjes in de gegeven string gebalanceerd zijn.
Bijvoorbeeld:
()geeft true terug())geeft false terug()()geeft true terug)(geeft false terug((geeft false terugabc(def(xy))zgeeft true teruga(bc(def(xy))zgeeft false terug
Longest common subsequence
Schrijf een recursieve methode String longestCommonSubsequence(String s1, String s2) die de langste reeks karakters teruggeeft die in beide strings in dezelfde volgorde terugkomen (niet noodzakelijk aaneensluitend). Als er meerdere oplossingen zijn, maakt het niet uit welke je teruggeeft.
Bijvoorbeeld:
longestCommonSubsequence("gitaarsnaar", "imaginair") == "ginar" of "ianar":gitaarsnaar
enimaginair
, ofgitaarsnaar
enimaginair
longestCommonSubsequence("aardappel", "adoptie") == "adpe":aardappel
enadoptie
Uitbreiding: zoek alle longest common subsequences tussen 2 strings.
Boomstructuur
Gegeven onderstaande record om een boomstructuur op te bouwen:
public record TreeNode<T>(T value, TreeNode<T> left, TreeNode<T> right){}
De boom
kan je hiermee aanmaken als:
var tree = new TreeNode<>("A",
new TreeNode<>("B",
new TreeNode<>("C", null, null),
new TreeNode<>("D", null, null)),
new TreeNode<>("E",
new TreeNode<>("F", null, null),
null));
- Schrijf een recursieve methode
int treeSize(TreeNode<?> tree)om het totale aantal knopen in de boom te berekenen. Voor de boom hierboven is de grootte 6. - Schrijf een recursieve methode
int treeHeight(TreeNode<?> tree)om de hoogte van de boom te berekenen. De hoogte is het maximum aantal stappen van de wortel (“A” hierboven) tot een kind (“C”, “D”, of “F”). In het voorbeeld is de hoogte dus 2. - Schrijf een recursieve methode
<T> void visitDepthFirstPreOrder(TreeNode<T> tree, Consumer<T> consumer)die de elementen van de boom overloopt in depth-first, pre-order volgorde. Dat houdt in: eerst de huidige knoop, dan de knopen van de linkertak (opnieuw in depth-first pre-order volgorde) en daarna die van de rechtertak. Voor de boom hierboven worden dus achtereenvolgens knopen “A”, “B”, “C”, “D”, “E”, en “F” bezocht en doorgegeven aan de consumer. Een voorbeeld van het gebruik van de methode om de knopen uit te printen:visitDepthFirstPreOrder(tree, System.out::print); System.out.println(); - Schrijf een recursieve methode
<T> void visitDepthFirstInOrder(TreeNode<T> tree, Consumer<T> consumer)die de elementen van de boom overloopt in depth-first, in-order volgorde. Dat houdt in: eerst de linkertak (in depth-first in-order volgorde), dan de knoop zelf, dan de rechtertak. Voor de boom hierboven worden dus achtereenvolgens knopen “C”, “B”, “D”, “A”, “F”, en “E” bezocht en doorgegeven aan de consumer. - Schrijf een recursieve methode
<T> TreeNode<T> mirrorTree(TreeNode<T> tree)om een willekeurige boom te spiegelen: het resultaat moet een nieuwe boom zijn, waar de linker-takken de rechtertakken geworden zijn en omgekeerd. De gespiegelde versie van de boom hierboven is dus:
- (extra) Schrijf een methode
String prettyPrint(TreeNode<?> tree)die een ASCII-voorstelling van de boom maakt. De voorbeeldboom wordt bijvoorbeeld:A | +-- B | | | +-- C | '-- D '-- E | +-- F
Stack omkeren
Schrijf een recursieve methode <T> void reverse(Deque<T> stack) die de volgorde van de items in een stack (Deque) omdraait, zonder gebruik te maken van een extra datastructuur (dus zonder een andere array, lijst, set, …).
Maak enkel gebruik van de isEmpty()-, pollFirst() en addFirst()-methodes van de Deque-interface.
var stack = new LinkedList<>(List.of("A", "B", "C", "D", "E", "F"));
System.out.println(stack); // [A, B, C, D, E, F]
reverse(stack);
System.out.println(stack); // [F, E, D, C, B, A]
Hint: je zal waarschijnlijk een hulpoperatie nodig hebben; die kan je ook recursief schrijven.
Toren van Hanoi (uitbreiding)
Los de toren van Hanoi op voor \( n\) schijven op 4 stapels (dus 2 hulpstapels). Je kan je oplossing manueel uittesten via deze simulator. (In de simulator moet je klikken, niet slepen)
Sorteren van een lijst
Schrijf een recursieve methode om een lijst van getallen te sorteren. De sortering moet in-place gebeuren (je past de lijst zelf aan door elementen van volgorde te wisselen, en geeft dus geen nieuwe lijst terug).
reduce
Schrijf een recursieve reduce-operatie die werkt op een lijst, naar analogie met de reduce-operatie op streams.
List<Integer> lst = List.of(1, 2, 3, 4);
int sum = reduce(lst, 0, (sum, x) -> sum + y); // sum == 10