8. Recursie en backtracking

8.1 Recursie

Wat is recursie?

Wiskundig gezien zijn recursieve functies functies die zichzelf één of meerdere keren oproepen. Een gekend voorbeeld is faculteit: $ n! = n \times (n-1)! $ met $ 0! = 1 $. Bijvoorbeeld:

$\begin{align} 5! & = 5 \times 4! \\\\ & = 5 \times (4 \times 3!) \\\\ & = 5 \times (4 \times (3 \times 2!)) \\\\ & = 5 \times (4 \times (3 \times (2 \times 1!))) \\\\ & = 5 \times (4 \times (3 \times (2 \times (1 \times 0!)))) \\\\ & = 5 \times (4 \times (3 \times (2 \times (1 \times 1)))) \\\\ & = 120 \end{align}$

Een ander gekend voorbeeld zijn de Fibonacci-getallen $ 0, 1, 1, 2, 3, 5, 8, 13, 21, \ldots $, gegeven door volgende recursieve vergelijking: $ F(n) = F(n-1) + F(n-2) $ met $ F(1) = 1 $ en $ F(0) = 0 $.

In Java kunnen we ook recursieve methodes definiëren. Hier is bijvoorbeeld een recursieve methode om de faculteit van een getal te berekenen:

public static int fac(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be non-negative");
  if (n == 0) return 1;
  return n * fac(n-1);
}

Merk op hoe dicht de implementatie aanleunt bij de wiskundige definitie. Dat geldt ook voor de methode om het n-de Fibonacci-getal te berekenen:

public static int fib(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be non-negative");
  if (n == 0) return 0;
  if (n == 1) return 1;
  return fib(n-1) + fib(n-2);
}

Merk op hoe de functie zichzelf tweemaal oproept.

De recursie eindigt wanneer een basisgeval bereikt wordt. Dat is een situatie (meestal een zeer eenvoudige) waar het antwoord onmiddellijk gekend is, en geen recursieve oproep meer nodig is. In bovenstaande code voor fib zijn de basisgevallen de oproepen waarin n kleiner is dan 2. We zouden ook een versie kunnen maken met meer basisgevallen; op zich maakt dat (buiten een klein beetje efficiëntie-winst) weinig verschil.

public static int fib_alt(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be non-negative");
  if (n == 0) return 0;
  if (n == 1) return 1;
  if (n == 2) return 1;
  if (n == 3) return 2;
  if (n == 4) return 3;
  if (n == 5) return 5;
  return fib_alt(n-1) + fib_alt(n-2);
}

Het belangrijkste bij een recursieve functie is dat de ketting van recursieve oproepen ooit eindigt. Volgende recursieve definitie van Fibonacci zou dus niet goed zijn:

Waarom niet?

public static int fib_bad(int n) {
  if (n == 0) return 0;
  return fib_bad(n-1) + fib_bad(n-2);
}

Recursie achter de schermen

Wanneer we een recursieve functie uitvoeren, doet Java achter de schermen heel wat boekhouding voor ons. Bekijk onderstaande illustratie die aangeeft wat er allemaal gebeurt om fib(5)=5 te berekenen:

graph TB
t[" "]
f5["return fib(4) + fib(3)"]
f4["return fib(3) + fib(2)"]
f3["return fib(2) + fib(1)"]
f2_1["return fib(1) + fib(0)"]
f2_2["return fib(1) + fib(0)"]
f1_1["return 1"]
f1_2["return 1"]
f1_3["return 1"]
f0_1["return 0"]
f0_2["return 0"]

f3_2["return fib(2) + fib(1)"]
f2_3["return fib(1) + fib(0)"]
f1_4["return 1"]
f1_5["return 1"]
f0_3["return 0"]

t --> |"fib(5)"| f5
f5 --> |"fib(4)"| f4
  f4 -->|"fib(3)"| f3
    f3 -->|"fib(2)"| f2_1
      f2_1 -->|"fib(1)"| f1_1
        f1_1 -->|1| f2_1
      f2_1 -->|"fib(0)"| f0_1
        f0_1 -->|0| f2_1
      f2_1 -->|1| f3
    f3 -->|"fib(1)"| f1_2
      f1_2 -->|1| f3
    f3 -->|2| f4
  f4 -->|"fib(2)"| f2_2
    f2_2 -->|"fib(1)"| f1_3
      f1_3 -->|1| f2_2
    f2_2 -->|"fib(0)"| f0_2
      f0_2 -->|0| f2_2
    f2_2 -->|1| f4
f5 --> |"fib(3)"| f3_2
  f3_2 -->|"fib(2)"| f2_3
      f2_3 -->|"fib(1)"| f1_4
        f1_4 -->|1| f2_3
      f2_3 -->|"fib(0)"| f0_3
        f0_3 -->|0| f2_3
      f2_3 -->|1| f3_2
    f3_2 -->|"fib(1)"| f1_5
      f1_5 -->|1| f3_2
    f3_2 -->|2| f5
f4 -->|3| f5
f5 -->|5| t

classDef base fill:#fcc,stroke:#933
class f0_1,f0_2,f0_3 base
class f1_1,f1_2,f1_3,f1_4,f1_5 base

Stack

De uitvoering van recursieve methodes maakt (net zoals de uitvoering van gewone methodes) gebruik van een stack. We herschrijven fib lichtjes om de uitleg te vergemakkelijken:

public static int fib(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be non-negative");
  if (n == 0) return 0;
  if (n == 1) return 1;
  int fib_n1 = fib(n-1);
  int fib_n2 = fib(n-2);
  int result = fib_n1 + fib_n2;
  return result;
}

Elke methode-oproep voegt een stackframe toe; in dat stackframe worden de waarden van alle parameters (bv. n voor fib hierboven) en lokale variabelen (fib_n1, fib_n2, en result) bewaard. Het bovenste stackframe is het actieve stackframe. Wanneer de methode-oproep voltooid is (bijvoorbeeld na het uitvoeren van een return-statement) verdwijnt dat stackframe, en wordt het vorige stackframe terug geactiveerd.

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
classDef active stroke:#363,fill:#afa
class f5 active

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
f5 --> f4
classDef active stroke:#363,fill:#afa
class f4 active

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
**fib_n1=???**
fib_n2=???
result=???`"]
f3["`**fib**
n=3
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
f5 --> f4
f4 --> f3
classDef active stroke:#363,fill:#afa
class f3 active

...

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
**fib_n1=???**
fib_n2=???
result=???`"]
f3["`**fib**
n=3
fib_n1=1
fib_n2=1
**result=2**`"]
main --> f5
f5 --> f4
f4 --> f3
classDef active stroke:#363,fill:#afa
class f3 active

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
fib_n1=2
**fib_n2=???**
result=???`"]
f3["`**fib**
n=3
fib_n1=1
fib_n2=1
result=2`"]
main --> f5
f5 --> f4
f4 ~~~ f3
classDef active stroke:#363,fill:#afa;
classDef removed stroke:#aaa,fill:#ddd,color:#aaa;
class f4 active
class f3 removed

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
fib_n1=2
**fib_n2=???**
result=???`"]
f2["`**fib**
n=2
**fib_n1=???**
fib_n2=???
result=???`"]
main --> f5
f5 --> f4
f4 --> f2
classDef active stroke:#363,fill:#afa
class f2 active

...

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
**fib_n1=???**
fib_n2=???
result=???`"]
f4["`**fib**
n=4
fib_n1=2
fib_n2=1
**result=3**`"]
main --> f5
f5 --> f4
classDef active stroke:#363,fill:#afa
class f4 active

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f4["`**fib**
n=4
fib_n1=2
fib_n2=1
result=3`"]
f5["`**fib**
n=5
fib_n1=3
**fib_n2=???**
result=???`"]
main --> f5
f5 ~~~ f4
classDef active stroke:#363,fill:#afa
classDef removed stroke:#aaa,fill:#ddd,color:#aaa;
class f5 active
class f4 removed

...

%%{init: {"flowchart": {"htmlLabels": false}} }%%
graph BT
main["`**main**`"]
f5["`**fib**
n=5
fib_n1=3
fib_n2=2
**result=5**`"]
main --> f5
classDef active stroke:#363,fill:#afa
class f5 active

Stack overflow

Zoals je hierboven kan zien, groeit de stack bij elke recursieve oproep. Elke stack-frame neemt een bepaalde hoeveelheid geheugen in. De totale grootte van de stack is echter beperkt. Wanneer de stack te groot wordt, krijg je een stack overflow. In Java uit zich dat door het gooien van een StackOverflowException.

Je kan de grootte die gereserveerd wordt voor de stack vergroten door bij de uitvoering een argument (-Xss) mee te geven aan de Java virtual machine (JVM). Bijvoorbeeld, om een stack van 4 megabyte te voorzien (de standaardgrootte is gewoonlijk 1 MB):

java -Xss4m Program

In IntelliJ kan je die optie toevoegen in de ‘Run configuration’.

Gewoonlijk zal dat niet nodig zijn; enkel wanneer je gebruik maakt van recursie voor grotere problemen. Een meer waarschijnlijke oorzaak van een StackOverflowException is een recursieve operatie die niet eindigt in een basisgeval.

Eindigheid en invoergrootte

Indien een recursieve methode niet zorgvuldig gedefinieerd wordt, bestaat de kans dat de recursie nooit stopt, en de methode dus nooit eindigt (tenzij met een StackOverflowException). Bijvoorbeeld, onderstaande recursieve methode bad

public static int bad(int n) {
  if (n == 0) return 0;
  return bad(n-2);
}

eindigt enkel voor positieve even getallen (overtuig jezelf hiervan).

Om er zeker van te zijn dat een recursieve methode ooit zal eindigen, moeten we kunnen aantonen dat elke recursieve oproep ooit een basisgeval zal bereiken. Dat is niet altijd eenvoudig of mogelijk. Neem bijvoorbeeld volgende welgekende functie van Collatz, gedefinieerd voor $ n \geq 1 $:

public static boolean collatz(int n) {
  if (n == 1) {
    return true;
  } else if (n % 2 == 0) { // n is even
    return collatz(n / 2);
  } else { // n is oneven > 1
    return collatz(3*n + 1);
  }
}

Wanneer we die uitvoeren voor n=5 krijgen we als waarden voor n achtereenvolgens 5, 16, 8, 4, 2, 1 en eindigt de recursie dus na 6 oproepen. Voor n=12 krijgen we 12, 6, 3, 10, 5, 16, 8, 4, 2, 1, en voor n=19 krijgen we 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1. De reeks waarden in deze voorbeelden lijkt dus steeds te eindigen op n=1, maar is dit zo voor elke beginwaarde van n? Er zijn geen gekende tegenvoorbeelden, maar er is ook geen bewijs dat dit het geval is voor elke beginwaarde van n.

Bewijzen dat een recursieve functie eindigt is echter wel vanzelfsprekend als elke recursieve oproep de grootte van de invoer strikt kleiner maakt, en de basisgevallen overeenkomen met de kleinst mogelijke invoergrootte(s). Aangezien een invoergrootte steeds (per definitie) een niet-negatief getal moet zijn, moet een voortdurende verkleining ervan ooit stoppen.

Typische invoergroottes bij recursieve problemen zijn

de waarde van een parameter, indien dit een natuurlijk getal is (bijvoorbeeld n in fib hierboven)
het aantal elementen in een datastructuur (lijst, set, …) die gebruikt wordt.

Maakt de collatz-methode de invoer steeds strikt kleiner?

Recursief denken

Recursie biedt vaak een erg krachtige manier om complexe algoritmische problemen op te lossen. Je moet hiervoor wel op de juiste manier redeneren over recursie. Een grote valkuil is nadenken over de volledige uitvoeringsboom, zoals we hierboven getoond hebben voor de Fibonacci-functie. De complexiteit hiervan is gigantisch, en staat een elegante oplossing en helder redeneren in de weg.

Een betere manier om na te denken over recursie gaat als volgt. Je wil een probleem van een bepaalde grootte $ n $ oplossen. Stel nu dat je mag veronderstellen dat je (magischerwijze) datzelfde probleem al kan oplossen, maar dan alleen voor alle (strikt kleinere) groottes $ n’ < n $. Hoe kan dit je helpen om het volledige probleem op te lossen? Met andere woorden, welke manieren zie je om een oplossing van een deel van het probleem te transformeren in een oplossing voor het hele probleem? Of nog anders gezegd: recursie gaat om vertrouwen: vertrouw erop dat het kleinere probleem juist opgelost wordt, en besteed enkel aandacht aan hoe je de oplossing voor een kleiner probleem kan gebruiken om de oplossing voor het grotere probleem te vinden. Eens je deze denkwijze onder de knie hebt, wordt recursie bijna een magisch stuk gereedschap.

We bekijken twee voorbeelden van deze denkwijze.

Voorbeeld 1: grootste element

Veronderstel dat je het grootste element uit een lijst van getallen wil bepalen (vergeet even dat we dat ook makkelijk kunnen met behulp van een lus). We noemen de lengte van die lijst $ n $. Stel nu dat we reeds beschikken over een magische oplossing (een functie) om het grootste element te vinden in alle lijsten met een lengte tot en met $ n-1 $. Hoe kunnen we deze oplossing gebruiken om het probleem op te lossen voor een lijst van lengte $ n $?

Denk hier even zelf over na!

Er zijn verschillende mogelijkheden. We weten bijvoorbeeld dat het grootste element ofwel het eerste element is, ofwel voorkomt in de rest van de lijst (alle elementen behalve het eerste). We kunnen onze magische functie dus gebruiken om het grootste element uit de rest van de lijst te zoeken, en dat vervolgens te vergelijken met het eerste. Dat leidt tot volgende recursieve implementatie:

public static int largestElement(List<Integer> list) {
    if (list.isEmpty()) throw new NoSuchElementException();
    if (list.size() == 1) return list.getFirst();

    var firstElement = list.getFirst();
    var largestRest = largestElement(list.subList(1, list.size()));
    return Math.max(firstElement, largestRest);
}

De basisgevallen hier zijn een lege lijst (er is dan geen grootste element) en een lijst met slechts één element (dat ene element moet het grootste element zijn). Merk op hoe we een subList gebruiken om makkelijk een kleinere lijst (zonder het element op index 0) te creëren voor de recursieve oproep. Zoals je je misschien herinnert, is het resultaat van subList een view op de originele lijst — er worden geen elementen gekopieerd. Dat is dus zeer efficiënt.

Er waren ook andere oplossingsstrategieën mogelijk met een gelijkaardige denkwijze. Bijvoorbeeld, we hadden het laatste element kunnen afzonderen in plaats van het eerste. Of we hadden het maximum van de eerste helft van de elementen kunnen vergelijken met het maximum van de tweede helft:

public static int largestElement_alt(List<Integer> list) {
    if (list.isEmpty()) throw new NoSuchElementException();
    if (list.size() == 1) return list.getFirst();

    int n = list.size();
    var largestFirstHalf = largestElement(list.subList(0, n/2));
    var largestSecondHalf = largestElement(list.subList(n/2, n));
    return Math.max(largestFirstHalf, largestSecondHalf);
}

Recursief denken lijkt voor dit voorbeeld misschien wat overbodig. Het maximum zoeken kan je inderdaad ook heel eenvoudig iteratief (met een for-lus). Daarom volgt een tweede voorbeeld, waar een iteratieve oplossing niet voor de hand ligt.

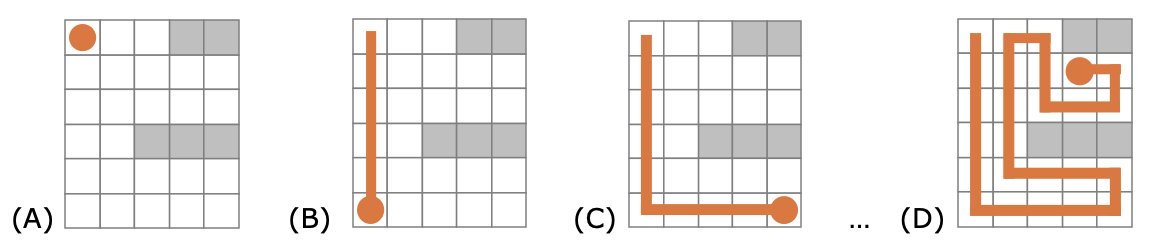
Voorbeeld 2: Toren van Hanoi

Je kent misschien de puzzel van de toren van Hanoi. We hebben drie stapels (A, B, en C), en op elke stapel mogen schijven liggen, van groot (onderaan) naar klein (bovenaan). De puzzel bestaat eruit om alle schijven van één stapel naar een andere te verplaatsen. Daarbij zijn er twee regels:

Je mag slechts 1 schijf per keer verplaatsen.
Een schijf mag nooit op een kleinere schijf terecht komen.

Hoe moeilijk/lang verwacht je dat een algoritme wordt om deze puzzel op te lossen?

Dit probleem wordt heel eenvoudig als we recursief denken. We moeten $ n $ schijven verplaatsen van een bronstapel (bijvoorbeeld A) naar een doelstapel (bijvoorbeeld C), en we hebben een extra stapel (B) die we als hulpstapel kunnen gebruiken. We vertrouwen er bovendien op dat we een magische oplossing (recursie!) hebben om $ n-1 $ (of minder) schijven te verplaatsen van een willekeurige stapel naar een andere willekeurige stapel, volgens de regels van de puzzel. Hoe kunnen we die magische oplossing gebruiken om het hele probleem op te lossen?

Denk hier zelf even over na!

We kunnen eerst de bovenste $ n-1 $ schijven verplaatsen van stapel A naar stapel B (de hulpstapel). De laatste overblijvende schijf op stapel A (de grootste schijf) verplaatsen we nu naar doelstapel C. Tenslotte verplaatsen we de $ n-1$ schijven van hulpstapel B ook naar doelstapel C (opnieuw via onze magische oplossing). Het basisgeval is heel eenvoudig: indien we 0 schijven moeten verplaatsen, doen we niets.

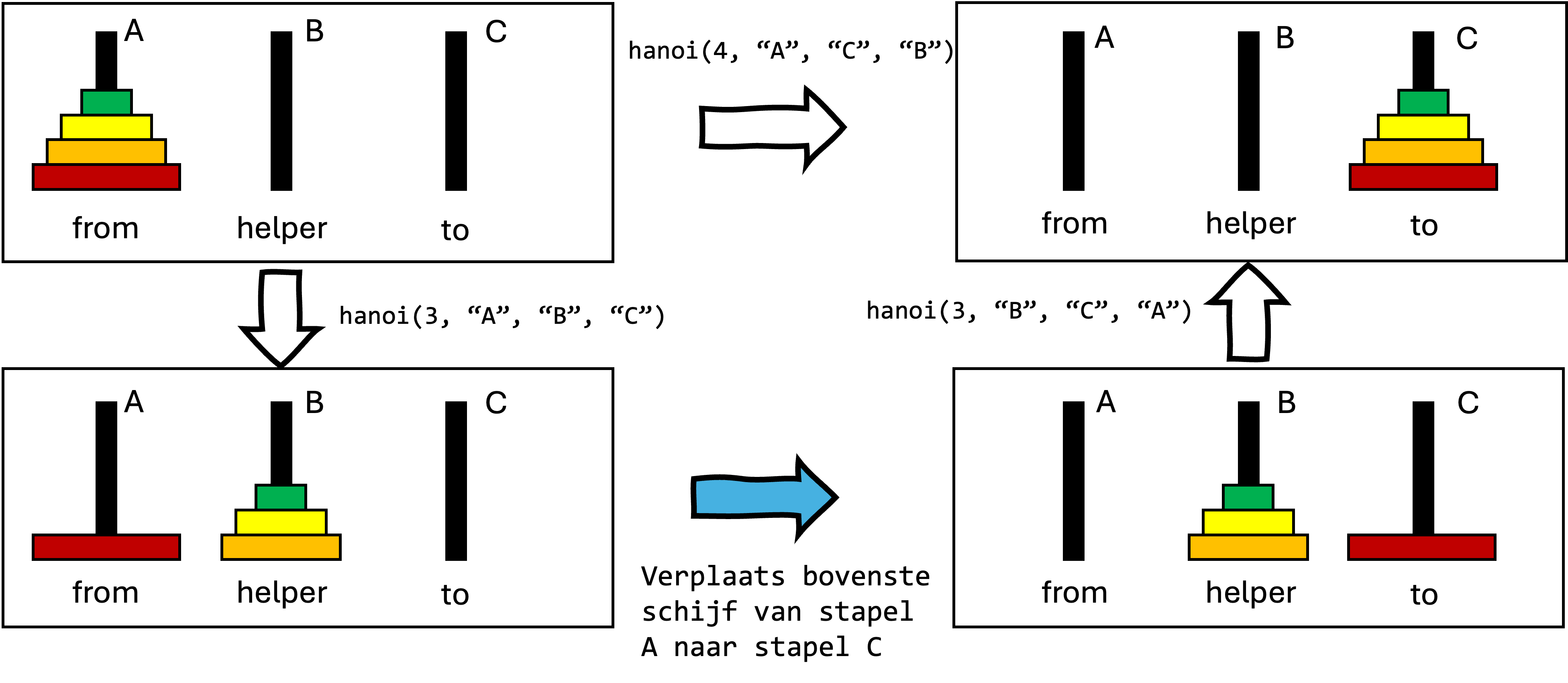
Dat geeft volgende oplossing in code, met n het aantal schijven en from, to, en helper de namen van de stapels, (bijvoorbeeld “A”, “B”, en “C”, of “links”, “midden”, en “rechts”):

public static void hanoi(int n, String from, String to, String helper) {
  if (n <= 0) return;
  hanoi(n-1, from, helper, to); // verplaats n-1 schijven van `from` naar `helper`, met `to` als hulpstapel
  System.out.println("Verplaats de bovenste schijf van stapel " + from + " naar stapel " + to);
  hanoi(n-1, helper, to, from); // verplaats n-1 schijven van `helper` naar `to`, met `from` als hulpstapel
}

Erg kort en elegant, niet?

Als we deze oplossing uitvoeren voor n=4 en from="A", to="C", en helper="B", krijgen we volgende uitvoer:

Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel C
Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel C naar stapel A
Verplaats de bovenste schijf van stapel C naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel A
Verplaats de bovenste schijf van stapel C naar stapel A
Verplaats de bovenste schijf van stapel B naar stapel C
Verplaats de bovenste schijf van stapel A naar stapel B
Verplaats de bovenste schijf van stapel A naar stapel C
Verplaats de bovenste schijf van stapel B naar stapel C

Ga na dat dit een correcte oplossing is voor het probleem, bijvoorbeeld via deze simulator.

Ter illustratie: de volledige uitvoeringsboom die bij bovenstaande uitvoer hoort ziet er als volgt uit; je leest de oplossing van boven naar onder af in de groene nodes. Het spreekt hopelijk voor zich dat denken over recursie in termen van zo’n bijhorende uitvoeringsboom niet de makkelijkste of duidelijkste manier is.

graph LR
H4ACB["1: hanoi(4,A,C,B)"]
H4ACBH3ABC["2: hanoi(3,A,B,C)"]
H4ACBH3ABCH2ACB["3: hanoi(2,A,C,B)"]
H4ACBH3ABCH2ACBH1ABC["4: hanoi(1,A,B,C)"]
H4ACBH3ABCH2ACBH1ABCH0ACB["5: hanoi(0,A,C,B)"]
H4ACBH3ABCH2ACBH1ABC --> H4ACBH3ABCH2ACBH1ABCH0ACB
H4ACBH3ABCH2ACBH1ABC --> H4ACBH3ABCH2ACBH1ABCm["6: Move A to B"]:::move
H4ACBH3ABCH2ACBH1ABCH0CBA["7: hanoi(0,C,B,A)"]
H4ACBH3ABCH2ACBH1ABC --> H4ACBH3ABCH2ACBH1ABCH0CBA
H4ACBH3ABCH2ACB --> H4ACBH3ABCH2ACBH1ABC
H4ACBH3ABCH2ACB --> H4ACBH3ABCH2ACBm["8: Move A to C"]:::move
H4ACBH3ABCH2ACBH1BCA["9: hanoi(1,B,C,A)"]
H4ACBH3ABCH2ACBH1BCAH0BAC["10: hanoi(0,B,A,C)"]
H4ACBH3ABCH2ACBH1BCA --> H4ACBH3ABCH2ACBH1BCAH0BAC
H4ACBH3ABCH2ACBH1BCA --> H4ACBH3ABCH2ACBH1BCAm["11: Move B to C"]:::move
H4ACBH3ABCH2ACBH1BCAH0ACB["12: hanoi(0,A,C,B)"]
H4ACBH3ABCH2ACBH1BCA --> H4ACBH3ABCH2ACBH1BCAH0ACB
H4ACBH3ABCH2ACB --> H4ACBH3ABCH2ACBH1BCA
H4ACBH3ABC --> H4ACBH3ABCH2ACB
H4ACBH3ABC --> H4ACBH3ABCm["13: Move A to B"]:::move
H4ACBH3ABCH2CBA["14: hanoi(2,C,B,A)"]
H4ACBH3ABCH2CBAH1CAB["15: hanoi(1,C,A,B)"]
H4ACBH3ABCH2CBAH1CABH0CBA["16: hanoi(0,C,B,A)"]
H4ACBH3ABCH2CBAH1CAB --> H4ACBH3ABCH2CBAH1CABH0CBA
H4ACBH3ABCH2CBAH1CAB --> H4ACBH3ABCH2CBAH1CABm["17: Move C to A"]:::move
H4ACBH3ABCH2CBAH1CABH0BAC["18: hanoi(0,B,A,C)"]
H4ACBH3ABCH2CBAH1CAB --> H4ACBH3ABCH2CBAH1CABH0BAC
H4ACBH3ABCH2CBA --> H4ACBH3ABCH2CBAH1CAB
H4ACBH3ABCH2CBA --> H4ACBH3ABCH2CBAm["19: Move C to B"]:::move
H4ACBH3ABCH2CBAH1ABC["20: hanoi(1,A,B,C)"]
H4ACBH3ABCH2CBAH1ABCH0ACB["21: hanoi(0,A,C,B)"]
H4ACBH3ABCH2CBAH1ABC --> H4ACBH3ABCH2CBAH1ABCH0ACB
H4ACBH3ABCH2CBAH1ABC --> H4ACBH3ABCH2CBAH1ABCm["22: Move A to B"]:::move
H4ACBH3ABCH2CBAH1ABCH0CBA["23: hanoi(0,C,B,A)"]
H4ACBH3ABCH2CBAH1ABC --> H4ACBH3ABCH2CBAH1ABCH0CBA
H4ACBH3ABCH2CBA --> H4ACBH3ABCH2CBAH1ABC
H4ACBH3ABC --> H4ACBH3ABCH2CBA
H4ACB --> H4ACBH3ABC
H4ACB --> H4ACBm["24: Move A to C"]:::move
H4ACBH3BCA["25: hanoi(3,B,C,A)"]
H4ACBH3BCAH2BAC["26: hanoi(2,B,A,C)"]
H4ACBH3BCAH2BACH1BCA["27: hanoi(1,B,C,A)"]
H4ACBH3BCAH2BACH1BCAH0BAC["28: hanoi(0,B,A,C)"]
H4ACBH3BCAH2BACH1BCA --> H4ACBH3BCAH2BACH1BCAH0BAC
H4ACBH3BCAH2BACH1BCA --> H4ACBH3BCAH2BACH1BCAm["29: Move B to C"]:::move
H4ACBH3BCAH2BACH1BCAH0ACB["30: hanoi(0,A,C,B)"]
H4ACBH3BCAH2BACH1BCA --> H4ACBH3BCAH2BACH1BCAH0ACB
H4ACBH3BCAH2BAC --> H4ACBH3BCAH2BACH1BCA
H4ACBH3BCAH2BAC --> H4ACBH3BCAH2BACm["31: Move B to A"]:::move
H4ACBH3BCAH2BACH1CAB["32: hanoi(1,C,A,B)"]
H4ACBH3BCAH2BACH1CABH0CBA["33: hanoi(0,C,B,A)"]
H4ACBH3BCAH2BACH1CAB --> H4ACBH3BCAH2BACH1CABH0CBA
H4ACBH3BCAH2BACH1CAB --> H4ACBH3BCAH2BACH1CABm["34: Move C to A"]:::move
H4ACBH3BCAH2BACH1CABH0BAC["35: hanoi(0,B,A,C)"]
H4ACBH3BCAH2BACH1CAB --> H4ACBH3BCAH2BACH1CABH0BAC
H4ACBH3BCAH2BAC --> H4ACBH3BCAH2BACH1CAB
H4ACBH3BCA --> H4ACBH3BCAH2BAC
H4ACBH3BCA --> H4ACBH3BCAm["36: Move B to C"]:::move
H4ACBH3BCAH2ACB["37: hanoi(2,A,C,B)"]
H4ACBH3BCAH2ACBH1ABC["38: hanoi(1,A,B,C)"]
H4ACBH3BCAH2ACBH1ABCH0ACB["39: hanoi(0,A,C,B)"]
H4ACBH3BCAH2ACBH1ABC --> H4ACBH3BCAH2ACBH1ABCH0ACB
H4ACBH3BCAH2ACBH1ABC --> H4ACBH3BCAH2ACBH1ABCm["40: Move A to B"]:::move
H4ACBH3BCAH2ACBH1ABCH0CBA["41: hanoi(0,C,B,A)"]
H4ACBH3BCAH2ACBH1ABC --> H4ACBH3BCAH2ACBH1ABCH0CBA
H4ACBH3BCAH2ACB --> H4ACBH3BCAH2ACBH1ABC
H4ACBH3BCAH2ACB --> H4ACBH3BCAH2ACBm["42: Move A to C"]:::move
H4ACBH3BCAH2ACBH1BCA["43: hanoi(1,B,C,A)"]
H4ACBH3BCAH2ACBH1BCAH0BAC["44: hanoi(0,B,A,C)"]
H4ACBH3BCAH2ACBH1BCA --> H4ACBH3BCAH2ACBH1BCAH0BAC
H4ACBH3BCAH2ACBH1BCA --> H4ACBH3BCAH2ACBH1BCAm["45: Move B to C"]:::move
H4ACBH3BCAH2ACBH1BCAH0ACB["46: hanoi(0,A,C,B)"]
H4ACBH3BCAH2ACBH1BCA --> H4ACBH3BCAH2ACBH1BCAH0ACB
H4ACBH3BCAH2ACB --> H4ACBH3BCAH2ACBH1BCA
H4ACBH3BCA --> H4ACBH3BCAH2ACB
H4ACB --> H4ACBH3BCA

classDef move stroke:green,fill:#afa

Recursie vs. iteratie

In sommige gevallen kan je een for- of while-lus eenvoudig herschrijven tot een recursieve methode en omgekeerd. Die omzetting volgt vaak eenzelfde patroon. Gegeven volgende while- of for-lus (in pseudocode):

R solve(input) {
  initialize result
  initialize helpers
  while (!finished) {
    update result and helpers
  }
  return result
}

R solve(input) {
  initialize result
  for (initialize helpers; !finished; update helpers) {
    update result
  }
  return result
}

kunnen we volgende equivalente recursieve versie schrijven (opnieuw in pseudo-code):

R solve(input) {
  return solve_worker(input, initialResult, initialHelpers);
}

R solve_worker(input, result, helpers) {
  if (finished) return result;
  update result and helpers
  return solve_worker((smaller) input, result, helpers);
}

Bijvoorbeeld, de iteratieve versie om faculteit te berekenen met een for-lus ziet er als volgt uit:

public int factorial(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be positive");
  int result = 1;
  for (int x = n; x > 0; x--) {
    result *= x;
  }
  return result;
}

En de bijhorende recursieve versie (volgens bovenstaand schema):

public int factorial(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be positive");
  return factorial_worker(n, 1);
}

private int factorial_worker(int x, int result) {
  if (x <= 0) return result;
  result *= x;
  x--;
  return factorial_worker(x, result);
}

De factorial_worker methode kunnen we ook nog wat korter schrijven:

public int factorial(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be positive");
  return factorial_worker(n, 1);
}

private int factorial_worker(int n, int result) {
  if (n == 0) return result;
  return factorial_worker(n - 1, n * result);
}

Deze recursieve oplossing bestaat uit 2 methodes; je herinnert je misschien nog dat de fac-methode aan het begin van deze pagina uit slechts 1 recursieve methode bestond:

public static int fac(int n) {
  if (n < 0) throw new IllegalArgumentException("n must be non-negative");
  if (n == 0) return 1;
  return n * fac(n-1);
}

Het verschil is dat we bij factorial gebruik maakten van het worker-wrapper patroon voor recursie. Dat patroon zie je vaak opduiken. De recursieve factorial_worker-methode (met 2 parameters) is de worker (daar gebeurt het eigenlijke werk), en de (niet-recursieve) factorial-methode met 1 parameter is de wrapper (die roept enkel de worker op met beginwaarden voor de extra parameters). Hulpvariabelen (hier het voorlopige resultaat, namelijk result) worden doorgegeven als parameters van de worker-methode. Die parameter wordt ook vaak de ‘accumulator’ genoemd, aangezien die het resultaat bijhoudt van al het werk dat tot dan toe gebeurd is.

De factorial_worker-methode is ook tail-recursive. Dat betekent dat de recursieve oproep de laatste bewerking is die gebeurt voor de functie eindigt (ze staat direct achter de ‘return’). In sommige programmeertalen (maar niet in Java) worden dergelijke tail-recursive oproepen geoptimaliseerd door de compiler: aangezien er geen werk meer uitgevoerd moet worden na de recursieve oproep, kan het stackframe meteen ook verwijderd worden. Je loopt dan geen risico op een stack overflow door teveel recursieve oproepen.

Efficiëntie

Wie goed kijkt naar de uitvoeringsboom van fib(5) hierboven kan zien dat er delen van de boom zijn die terugkeren. Bijvoorbeeld, fib(3) wordt tweemaal opnieuw berekend, fib(2) driemaal, en fib(1) komt vijfmaal voor. Dat is natuurlijk niet erg efficiënt.

Technieken zoals ‘dynamisch programmeren’ (dynamic programming) en memoization kunnen hier soelaas bieden. We gebruiken deze technieken niet verder binnen deze cursus, maar illustreren hier kort even het achterliggende idee.

Een voorbeeld van hoe memoization gebruikt kan worden voor Fibonacci gaat als volgt (merk op dat we ook het worker-wrapper patroon gebruiken):

public static int fib(int n) {
    if (n < 0) throw new IllegalArgumentException();
    int[] memo = new int[n+1];
    Arrays.fill(memo, -1);
    return fib_memoized(n, memo);
}

private static int fib_memoized(int n, int[] memo) {
    var result = memo[n];
    if (result == -1) {
        if (n == 0) result = 0;
        else if (n == 1) result = 1;
        else result = fib_memoized(n-1, memo) + fib_memoized(n-2, memo);
        memo[n] = result;
    }
    return result;
}

We maken gebruik van een array memo. Initieel zijn alle elementen daarvan gelijk aan -1, wat hier betekent dat ze nog niet berekend zijn. Telkens het n-de Fibonacci-getal berekend wordt, slaan we het op op plaats memo[n]. Wanneer dit getal later opnieuw opgevraagd wordt, berekenen we het niet opnieuw, maar herbruiken we gewoon het resultaat van de vorige keer.

Voor $ n=20 $ gebeuren er in de gewone implementatie 6765 oproepen van de fib-methode. De versie met memoization doet in totaal 39 oproepen van fib_memoized; alle andere oproepen werden vervangen door het uitlezen van het resultaat uit de memo-array.

Je kan dit nog verder optimaliseren: je weet dat elke oproep alleen de vorige twee waarden nodig heeft: om het n-de fibonacci-getal te berekenen heb je enkel het (n-1)‘ste en (n-2)‘de fibonacci-getal nodig. Je hoeft dus niet alle waarden bij te houden in een array, enkel de laatste twee (dat kan met twee variabelen). En in plaats van te vertrekken bij het n-de Fibonacci-getal en naar kleinere Fibonacci-getallen te gaan, kunnen we ook beginnen bij de kleinste Fibonacci-getallen en omhoog gaan tot we uiteindelijk bij het n-de uitkomen.

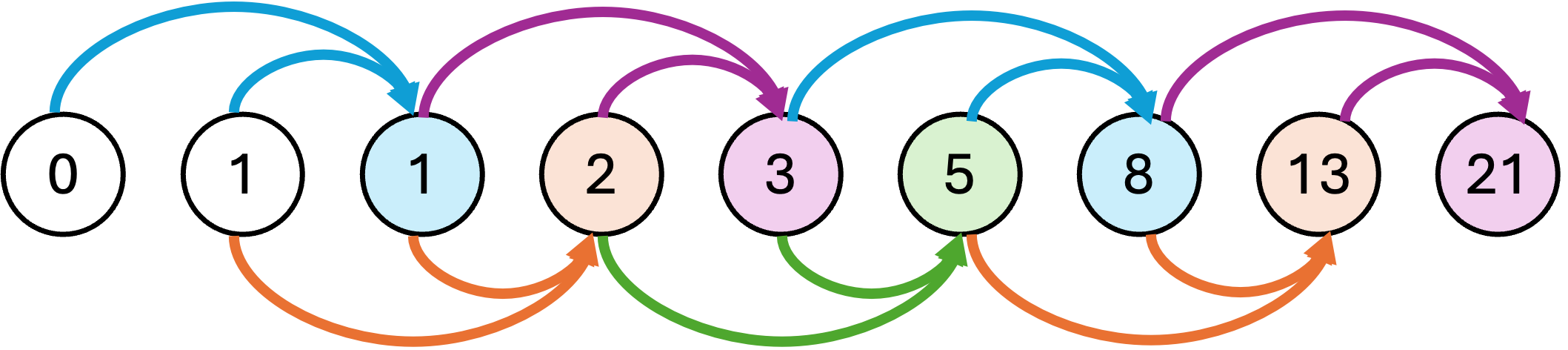
Dat leidt tot volgende recursieve oplossing (opnieuw met het worker-wrapper patroon), waar prevprev en prev de vorige twee waarden voorstellen.

public static int fib(int n) {
    if (n < 0) throw new IllegalArgumentException();
    if (n == 0) return 0;
    if (n == 1) return 1;
    return fib_worker(n, 2, 0, 1); // n >= 2
}
private static int fib_worker(int targetN, int currentN, int prevprev, int prev) {
    if (currentN == targetN) return prevprev + prev; // fib(n-2) + fib(n-1)
    return fib_worker(targetN, currentN+1, prev, prevprev+prev);
}

Hieronder zie je de oproepen van fib_worker om fib(6) te berekenen.

targetN	currentN	prevprev	prev	returns
6	2	0	1	`fib_worker(6, 3, 1, 0+1=1)`
6	3	1	1	`fib_worker(6, 4, 1, 1+1=2)`
6	4	1	2	`fib_worker(6, 5, 2, 1+2=3)`
6	5	2	3	`fib_worker(6, 6, 3, 2+3=5)`
6	6	3	5	`3 + 5 = 8`

Deze versie kan ook makkelijk iteratief geschreven worden:

public static int fib(int n) {
    if (n < 0) throw new IllegalArgumentException();
    if (n == 0) return 0;
    if (n == 1) return 1;
    int prevprev = 0;
    int prev = 1;
    for (int x = 2; x != n; x++) {
      int newprevprev = prev;
      int newprev = prevprev + prev;
      prevprev = newprevprev;
      prev = newprev;
    }
    return prevprev + prev;
}

Onderzoek de gelijkenissen en verschillen tussen de recursieve en iteratieve versie.

Patronen om het probleem te verkleinen

Zoals eerder gezegd, gaan we bij recursie kijken of/hoe de oplossing voor hetzelfde maar kleiner probleem ons kan helpen om het volledige probleem op te lossen. Er zijn enkele vaak voorkomende manieren om dat te doen, die we hier kort oplijsten. Alle manieren komen in essentie natuurlijk op hetzelfde neer: een geschikt deelprobleem zoeken dat je helpt om het volledige probleem op te lossen.

Een numerieke parameter rechtstreeks verkleinen. Bijvoorbeeld, de oplossing voor parameter x berekenen aan de hand van de oplossing voor x-1, x-2, x/2, …
Het eerste/laatste element van de invoer weglaten. Bijvoorbeeld, de oplossing voor de hele invoerlijst lst berekenen aan de hand van de oplossing voor de invoerlijst maar dan zonder het eerste of laatste element (bv. lst.subList(1, lst.size()))). Hetzelfde idee kan je toepassen op Strings (met substring).
De invoer halveren. Bijvoorbeeld, de oplossing voor de hele lijst lst berekenen aan de hand van de oplossing voor de eerste en tweede helft van de invoerlijst (bv. lst.subList(0, lst.size()/2)). Ook dit idee kan toegepast worden op Strings (met substring).
Twee situaties beschouwen. Dit is een variant van het weglaten van het eerste/laatste element die vooral handig is bij problemen waar de oplossing gevormd wordt met een combinatie van sommige invoerelementen. Je beschouwt dan twee deelproblemen:
1. je zoekt eerst naar een oplossing waarbij je ervan uitgaat dat het eerste (of laatste, middelste, …) element deel uitmaakt van de oplossing.
2. Daarnaast zoek je ook naar een oplossing waarbij je ervan uitgaat dat dat element geen deel uitmaakt van de oplossing.
Voor elk van die twee situaties los je dan een kleiner (en waarschijnlijk aangepast) probleem op waarbij je verder geen rekening meer houdt met dat ene element. Achteraf combineer je de oplossingen voor beide deelproblemen op een gepaste manier. Zie de oefeningen voor concrete voorbeelden (in het bijzonder de oefening over gepast betalen).

Recursie: oefeningen

Je vind tests en skelet-code voor de oefeningen rond recursie op Github.

Palindroom

Schrijf een recursieve functie isPalindrome die nagaat of een String een palindroom is. Een String is een palindroom als die hetzelfde is van links naar rechts als van rechts naar links, bijvoorbeeld

racecar
level
deified
lepel
droomoord
redder
meetsysteem
koortsmeetsysteemstrook

String omkeren

Schrijf een recursieve methode reverse om een String om te keren, bijvoorbeeld:

Hello -> olleH
racecar -> racecar

Element zoeken in lijst

Schrijf een recursieve functie <T> int search(List<T> list, T element) die nagaat of het gegeven element voorkomt in de gegeven lijst. Als het element voorkomt, wordt de index teruggegeven, anders -1.

Maak eerst een versie die werkt voor een willekeurige (niet-gesorteerde) lijst.
Maar vervolgens een snellere versie die werkt voor een gesorteerde lijst, door het te doorzoeken stuk van de lijst telkens halveert en slechts in één van die helften verder gaat zoeken. (Dit is ‘binary search’)

Duplicaten verwijderen

Schrijf een recursieve methode removeDuplicateCharacters die opeenvolgende dezelfde karakters uit een String verwijdert. Bijvoorbeeld:

aaaaa -> a
koortsmeetsysteemstrook -> kortsmetsystemstrok
AAAbbCdddAAA -> AbCdA

Greatest common divisor

Schrijf een functie gcd die de grootste gemene deler bepaalt tussen twee getallen. Maak gebruik van het feit dat, als $ x \geq y $, dat dan $ \gcd(x, y) = \gcd(y, x \% y) $ met % de modulo-operatie, en dat $ \gcd(x, 0) = x $.

Snelle macht

Schrijf een recursieve functie double power(double x, int n) die $ x^n $ berekent met zo weinig mogelijk berekeningen. Maak gebruik van het feit dat $ x^{2n} = x^n \cdot x^n $ en $ x^{2n+1} = x \cdot x^{2n} $.

Sum of digits

Schrijf een recursieve methode int sumOfDigits(long number) die de som van de cijfers van een (niet-negatief) getal berekent, en dat herhaalt tot die som kleiner is dan 10. Bijvoorbeeld: 62984 geeft 6+2+9+8+4 = 29; dat wordt vervolgens 2+9 = 11; en dat wordt uiteindelijk 1+1 = 2. Het resultaat is dus 2.

Trap beklimmen

Schrijf een functie om te berekenen hoeveel verschillende manieren er zijn om een trap met $ n $ treden op te gaan, als je bij elke stap kan kiezen om 1 of 2 treden tegelijk te nemen. Bijvoorbeeld, een trap met $ n = 4 $ treden kan je op 5 verschillende manieren beklimmen:

1 trede, 1 trede, 1 trede, 1 trede
1 trede, 1 trede, 2 treden
1 trede, 2 treden, 1 trede
2 treden, 1 trede, 1 trede
2 treden, 2 treden

Gepast betalen

Schrijf een recursieve methode boolean kanGepastBetalen(int bedrag, List<Integer> munten) die nagaat of je het gegeven bedrag (uitgedrukt in eurocent) gepast kan betalen met (een deel van) de gegeven munten (en briefjes). Elke munt in de lijst mag slechts één keer gebruikt worden. Bijvoorbeeld:

kanGepastBetalen(20, List.of(50, 10, 10, 5)) geeft true terug, want 10+10 = 20.
kanGepastBetalen(125, List.of(100, 100, 50, 20, 10, 5 )) geeft true terug, want 100+20+5 = 125.
kanGepastBetalen(260, List.of(100, 100, 50, 20, 5 )) geeft false terug: er is geen combinatie van munten die samen 260 geeft.

Gepast betalen (bis)

Gegeven een lijst van muntwaarden (bv. 5, 10, 20, 50, 100, 200), schrijf een recursieve methode int countChange(int amount, List<Integer> coinValues) die bepaal op hoeveel manieren je een specifiek bedrag kan betalen. Je mag nu veronderstellen dat je een voldoende aantal (of oneindig veel) munten van elke opgegeven waarde hebt.

Bijvoorbeeld, met bovenstaande muntwaarden

kan je een bedrag van 35 betalen op 6 manieren:
- 7×5
- 1×10 en 5×5
- 1×10 en 1×20 en 1×5
- 2×10 en 3×5
- 3×10 en 1×5
- 1×20 en 3×5
kan je een bedrag van 260 betalen op 646 manieren
kan je een bedrag van 1000 betalen op 98411 manieren

Alle prefixen van een String

Schrijf een recursieve functie allPrefixes die een Set teruggeeft met alle prefixen van een gegeven String. Bijvoorbeeld:

allPrefixes("cat") == { "", "c", "ca", "cat" }
allPrefixes("Hello") == { "", "H", "He", "Hel", "Hell", "Hello" }

Alle interleavings van twee strings

Schrijf een recursieve functie allInterleavings(String s1, String s2) die een Set teruggeeft met alle interleavings van de twee strings s1 en s2. Een interleaving is een nieuwe string met daarin alle karakters van de eerste en de tweede string, in dezelfde volgorde waarin ze in elk van de originele strings voorkomen, maar mogelijk door elkaar. Bijvoorbeeld:

allInterleavings("A", "B") = [AB, BA]
allInterleavings("ABC", "x") = [ABCx, ABxC, AxBC, xABC]
allInterleavings("AB", "xy") = [ABxy, AxBy, AxyB, xABy, xAyB, xyAB]
allInterleavings("ABC", "xy") = [ABCxy, ABxCy, ABxyC, AxBCy, AxByC, AxyBC, xABCy, xAByC, xAyBC, xyABC]

Vliegtuigreis

Gegeven een record Item:

record Item(String name, int weight, int value) {}

wat een item voorstelt dat je mee wil nemen op reis. Het item heeft een naam, een gewicht, en een waarde (hoe graag je het mee wil).

Schrijf een methode List<Item> pack(List<Item> choices, int maxWeight) die een keuze maakt uit de gegeven lijst van items, zodanig dat de items met een zo groot mogelijke totaalwaarde kan meenemen zonder dat het totale gewicht hoger wordt dan het maximumgewicht (opgelegd door de vliegtuigmaatschappij).

Bijvoorbeeld, met vier items (A, 50kg, 10), (B, 20kg, 5), (C, 10kg, 2), en (D, 5kg, 1):

met een totaal toegelaten gewicht van 100kg kan je alle items meenemen, voor een totale waarde van 18;
met een totaal toegelaten gewicht van 60kg kan je best items A en C meenemen, voor een totale waarde van 12;
met een totaal toegelaten gewicht van 20kg kan je best item B meenemen, voor een totale waarde van 5;

Powerset

Schrijf een recursieve functie Set<Set<T>> powerset(Set<T> s) die de powerset berekent van de gegeven set s. De powerset is de set van alle deelverzamelingen van s. Bijvoorbeeld:

powerset(Set.of("A", "B")) = [[], [A], [B], [A, B]]
powerset(Set.of("A", "B", "C")) = [[], [A], [B], [C], [A, B], [A, C], [B, C], [A, B, C]]

Alle permutaties van een lijst berekenen

Schrijf een functie allPermutations die een Set teruggeeft met alle permutaties van een gegeven lijst. Bijvoorbeeld:

allPermutations(List.of("A", "B")) = [ [A, B], [B, A] ]
allPermutations(List.of("A", "B", "C")) = [ [A, B, C], [A, C, B], [B, A, C], [B, C, A], [C, A, B], [C, B, A] ]

Gebalanceerde haakjes

Schrijf met behulp van recursie een methode boolean balancedParentheses(String s) die nagaat of alle haakjes in de gegeven string gebalanceerd zijn. Bijvoorbeeld:

() geeft true terug
()) geeft false terug
()() geeft true terug
)( geeft false terug
(( geeft false terug
abc(def(xy))z geeft true terug
a(bc(def(xy))z geeft false terug

Hint: gebruik het worker-wrapper-patroon, en denk (in plaats van ‘is deze string gebalanceerd’) aan een andere (gerelateerde) vraag die wél nuttig kan zijn om het probleem recursief op te lossen.

Longest common subsequence

Schrijf een recursieve methode String longestCommonSubsequence(String s1, String s2) die de langste reeks karakters teruggeeft die in beide strings in dezelfde volgorde terugkomen (niet noodzakelijk aaneensluitend). Als er meerdere oplossingen zijn, maakt het niet uit welke je teruggeeft.

Bijvoorbeeld:

longestCommonSubsequence("gitaarsnaar", "imaginair") == "ginar" of "ianar":
```
gitaarsnaar
```
en
```
imaginair
```
, of
```
gitaarsnaar
```
en
```
imaginair
```
longestCommonSubsequence("aardappel", "adoptie") == "adpe":
```
aardappel
```
en
```
adoptie
```
longestCommonSubsequence("sterrenstelselsamenstellingsanalyseinstrument", "restaurantkeukenapparatuurontwerpmethodiek") == "restantenaantrmet" (met dank aan ChatGPT voor de suggestie):
```
sterrenstelselsamenstellingsanalyseinstrument
```
en
```
restaurantkeukenapparatuurontwerpmethodiek
```

Het laatste voorbeeld zal waarschijnlijk veel te lang duren. Je kan nadenken of je je algoritme wat ‘slimmer’ kan maken.

Boomstructuur

Gegeven onderstaande record om een boomstructuur op te bouwen:

public record TreeNode<T>(T value, TreeNode<T> left, TreeNode<T> right){}

De boom

kan je hiermee aanmaken als:

var tree = new TreeNode<>("A",
              new TreeNode<>("B",
                new TreeNode<>("C", null, null),
                new TreeNode<>("D", null, null)),
              new TreeNode<>("E",
                new TreeNode<>("F", null, null),
                null));

Schrijf een recursieve methode int treeSize(TreeNode<?> tree) om het totale aantal knopen in de boom te berekenen. Voor de boom hierboven is de grootte 6.
Schrijf een recursieve methode int treeHeight(TreeNode<?> tree) om de hoogte van de boom te berekenen. De hoogte is het maximum aantal stappen van de wortel (“A” hierboven) tot een kind (“C”, “D”, of “F”). In het voorbeeld is de hoogte dus 2.
Schrijf een recursieve methode <T> void visitDepthFirstPreOrder(TreeNode<T> tree, Consumer<T> consumer) die de elementen van de boom overloopt in depth-first, pre-order volgorde. Dat houdt in: eerst de huidige knoop, dan de knopen van de linkertak (opnieuw in depth-first pre-order volgorde) en daarna die van de rechtertak. Voor de boom hierboven worden dus achtereenvolgens knopen “A”, “B”, “C”, “D”, “E”, en “F” bezocht en doorgegeven aan de consumer. Een voorbeeld van het gebruik van de methode om de knopen uit te printen:
```
visitDepthFirstPreOrder(tree, System.out::print);
System.out.println();
```
Schrijf een recursieve methode <T> void visitDepthFirstInOrder(TreeNode<T> tree, Consumer<T> consumer) die de elementen van de boom overloopt in depth-first, in-order volgorde. Dat houdt in: eerst de linkertak (in depth-first in-order volgorde), dan de knoop zelf, dan de rechtertak. Voor de boom hierboven worden dus achtereenvolgens knopen “C”, “B”, “D”, “A”, “F”, en “E” bezocht en doorgegeven aan de consumer.
Schrijf een recursieve methode <T> TreeNode<T> mirrorTree(TreeNode<T> tree) om een willekeurige boom te spiegelen: het resultaat moet een nieuwe boom zijn, waar de linker-takken de rechtertakken geworden zijn en omgekeerd. De gespiegelde versie van de boom hierboven is dus:

(extra) Schrijf een methode String prettyPrint(TreeNode<?> tree) die een ASCII-voorstelling van de boom maakt. De voorbeeldboom wordt bijvoorbeeld:
```
A
|
+-- B
|   |
|   +-- C
|   '-- D
'-- E
    |
    +-- F
```

Stack omkeren

Schrijf een recursieve methode <T> void reverse(Deque<T> stack) die de volgorde van de items in een stack (Deque) omdraait, zonder gebruik te maken van een extra datastructuur (dus zonder een andere array, lijst, set, …). Maak enkel gebruik van de isEmpty()-, pollFirst() en addFirst()-methodes van de Deque-interface.

var stack = new LinkedList<>(List.of("A", "B", "C", "D", "E", "F"));
System.out.println(stack); // [A, B, C, D, E, F]
reverse(stack);
System.out.println(stack); // [F, E, D, C, B, A]

Hint: overweeg een (recursieve) hulpoperatie om een element onderaan de stack in te voegen.

Toren van Hanoi (uitbreiding)

Los de toren van Hanoi op voor $ n$ schijven op 4 stapels (dus 2 hulpstapels). Je kan je oplossing manueel uittesten via deze simulator. (In de simulator moet je klikken, niet slepen)

Sorteren van een lijst

Schrijf een recursieve methode om een lijst van getallen te sorteren. De sortering moet in-place gebeuren (je past de lijst zelf aan door elementen van volgorde te wisselen, en geeft dus geen nieuwe lijst terug).

reduce

Schrijf een recursieve reduce-operatie die werkt op een lijst, naar analogie met de reduce-operatie op streams.

List<Integer> lst = List.of(1, 2, 3, 4);
int sum = reduce(lst, 0, (sum, x) -> sum + y); // sum == 10

8.2 Backtracking

Wat is backtracking?

Backtracking is een techniek om oplossingen te zoeken voor een probleem. Een eenvoudig voorbeeld waar je backtracking kan toepassen is de weg zoeken in een doolhof: op elke splitsing waar je kan kiezen welke richting je uitgaat, maak je een keuze. Als je later niet meer verder blijkt te kunnen, keer je terug naar die splitsing en probeer je een van de andere richtingen.

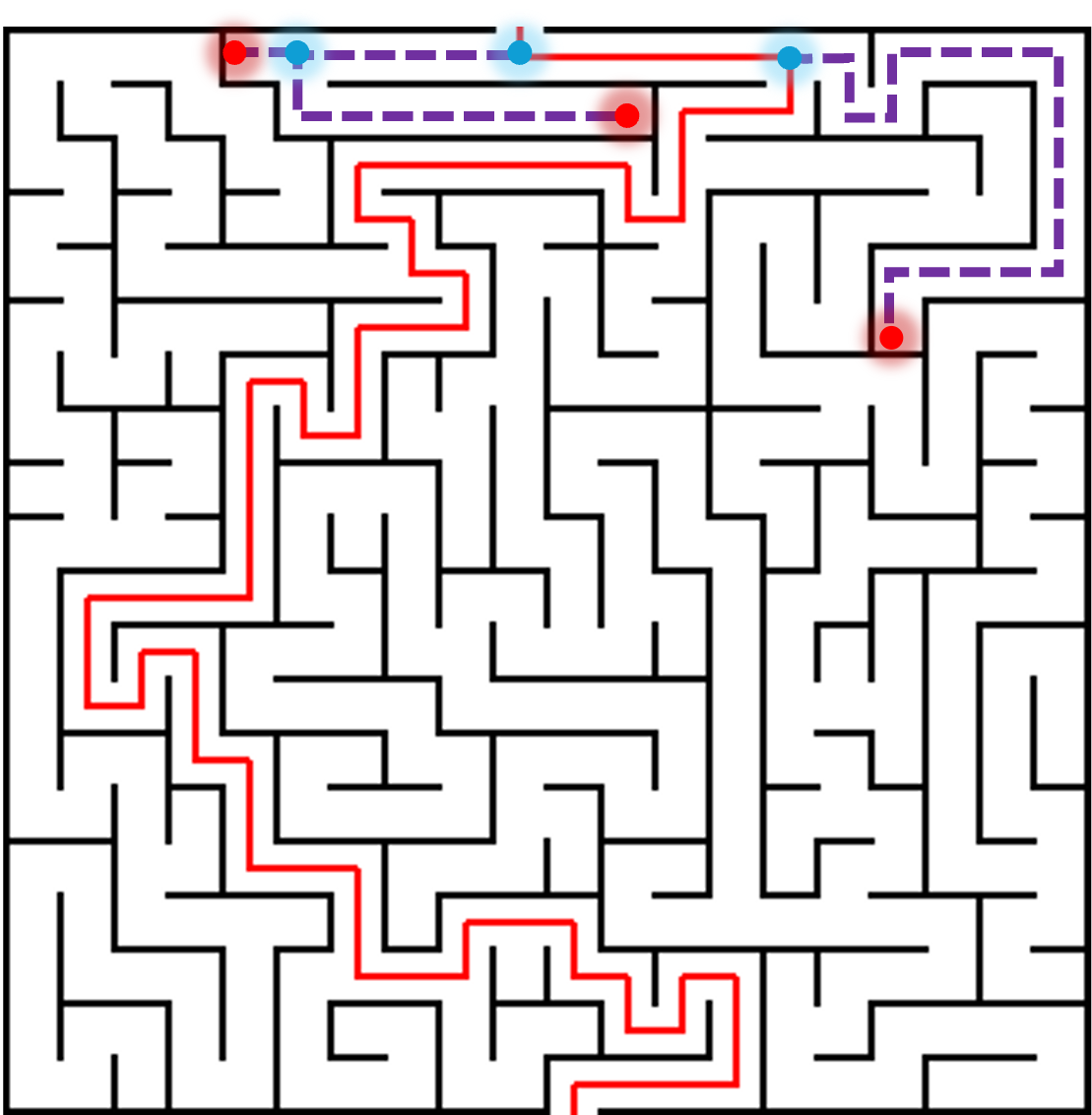
Meer algemeen werkt een backtracking-algoritme als volgt:

je vertrekt van een gedeeltelijke oplossing (in het begin is die leeg). In het voorbeeld van de doolhof: het pad dat je al afgelegd hebt om tot bij een splitsing te komen.
je breidt die gedeeltelijke oplossing stapsgewijs uit naar een volledige(re) oplossing, waar je bij elke uitbreiding een keuze maakt. Wanneer die keuze later niet blijkt te leiden tot een geschikte oplossing, keer je terug naar dat keuzepunt (backtracking) en maak je een andere keuze. In het voorbeeld van de doolhof: als je vastzit, keer keer je terug naar de vorige splitsing, en je kiest een andere gang. Als je alle gangen geprobeerd hebt zonder resultaat, keer je terug naar de splitsing daarvoor, etc.

Een backtracking-algoritme maakt meestal gebruik van recursie. De stack die impliciet gebruikt wordt bij recursie is immers heel handig om bij te houden welke keuzes al gemaakt werden, en in welke volgorde.

Voorbeeld: token segmentatie

Het token segmentatie probleem bestaat erin na te gaan of je een gegeven string kan bekomen als sequentie van een of meerdere tokens uit een gegeven lijst van tokens. Bijvoorbeeld: voor de string "catsanddogs" en de tokenlijst [s, an, ca, cat, dog, and, sand, dogs] zijn volgende segmentaties mogelijk:

cat sand dogs
cat sand dog s
cat s and dog s
cat s and dogs

Met dezelfde woordenlijst kan de string acatandadog niet gesegmenteerd worden.

We bespreken hieronder hoe we dit probleem kunnen oplossen met backtracking. We beschouwen drie varianten:

uitzoeken of er minstens één segmentatie bestaat (en die teruggeven)
alle mogelijke segmentaties teruggeven
de segmentatie die het minst aantal tokens gebruikt teruggeven.

Eén (willekeurige) oplossing zoeken

De essentie van een backtracking-algoritme is het zoeken van één oplossing. Dit ligt ook aan de basis van de andere twee varianten (zoeken van alle oplossingen en zoeken van een optimale oplossing). Het achterliggend idee is zeer eenvoudig: probeer telkens iets, en als dat niet tot een oplossing leidt, keer terug en probeer iets anders, tot je een oplossing gevonden hebt of alles geprobeerd hebt (dan is er geen oplossing). We bekijken nu hoe we dit idee concreet kunnen beschrijven met een algoritme.

Voorbeeld: token segmentatie

Stel: we willen voor het segmentatie-probleem een (willekeurige) oplossing teruggeven (als die bestaat). De oplossing zoeken met een backtracking-algoritme zal, zoals gezegd, gebaseerd zijn op recursie. Dus: om token segmentatie voor een string van lengte $ n $ te doen, veronderstellen we dat we dit al kunnen oplossen voor alle strings van lengte $ n' < n $. Het basisgeval is een lege string segmenteren; we moeten dan geen tokens gebruiken.

We moeten nu enkel nog nadenken over hoe een oplossing voor een kortere string ons precies kan helpen om het hele probleem op te lossen.

Denk hier zelf even over na

Hier is een idee: wat als we, voor elke mogelijke token, nagaan of die overeenkomt met het begin van de string, en als dat zo is, die token wegknippen uit het begin van de string? Zo wordt de string korter, en kunnen we recursie gebruiken om het probleem verder op te lossen voor die kortere string. De oplossing voor het hele probleem bestaat dan uit de weggeknipte token, gevolgd door de tokens die nodig zijn om de kortere string op te bouwen (die bekomen we via de recursie).

We maken dus telkens één keuze, namelijk welk token (uit de lijst van mogelijke tokens) we proberen te matchen met het begin van de string.

Hieronder zie je een zoekboom die een mogelijke uitvoering van dat idee weergeeft voor de string catsanddogs en de tokenlijst [s, an, ca, cat, dog, and, sand, dogs]. Om die te begrijpen, beginnen we bovenaan. In de rechthoeken staat telkens de lijst van tokens die we tot dan toe gekozen hebben, en de resterende string. In het begin hebben we nog geen tokens gekozen ([]), en is de resterende string nog gelijk aan de volledige string catsanddogs. De pijltjes geven aan welke token we kiezen (we tonen enkel de tokens die overeenkomen met het begin van de string; de anderen leiden sowieso tot niets). We volgen steeds eerst de linkerpijl naar beneden. De gestippelde lijnen geven aan waar we backtracken.

Een situatie die niet tot een oplossing kan leiden (geen enkele token komt overeen met het begin van de string) wordt rood gekleurd; we gaan dan terug een knoop naar boven en nemen de volgende tak. De gevonden oplossing wordt in het groen aangeduid. Eens deze gevonden is, zoeken we niet meer verder.

graph TB

start["[], catsanddogs"]
start -->|ca| ca
ca["[ca], tsanddogs"]
class ca fail
ca -.-> start
start -->|cat| cat
cat["[cat], sanddogs"]
cat -->|s| cat_s
cat_s["[cat, s], anddogs"]
cat_s -->|an| cat_s_an
cat_s_an["[cat, s, an], ddogs"]
class cat_s_an fail
cat_s_an -.-> cat_s
cat_s -->|and| cat_s_and
cat_s_and["[cat, s, and], dogs"]
cat_s_and -->|dog| cat_s_and_dog
cat_s_and_dog["[cat, s, and, dog], s"]
cat_s_and_dog -->|s| cat_s_and_dog_s
cat_s_and_dog_s["[cat, s, and, dog, s], "]
class cat_s_and_dog_s success

classDef success fill:#2c2,stroke:#393,stroke-width:3,color:white;
classDef fail fill:#c22,stroke:#933,stroke-width:3,color:white;

De informatie in de rechthoeken stelt de gedeeltelijke/partiële oplossing voor die we bijhouden. Die bevat hier dus twee zaken:

de reeds gebruikte token-sequentie (initieel een lege lijst)
het deel van de string dat nog overblijft (initieel de hele string)

Nadat we een token gekozen hebben, moeten we deze gedeeltelijke oplossing uitbreiden (aanpassen) op basis van die keuze. Om dat te doen, moeten we

nakijken of het gekozen token voorkomt aan het begin van de resterende string
dat token toevoegen aan de lijst van gebruikte tokens
de resterende string inkorten, door het token vooraan te verwijderen

Eens we dat gedaan hebben, kiezen we opnieuw een token en doen we hetzelfde. Die herhaling gebeurt door middel van recursie.

We hebben een oplossing gevonden wanneer het overblijvende deel van de string leeg is.

Als later zou blijken dat een gemaakte keuze fout was (dus dat we met die keuze niet tot een oplossing komen), moeten we deze keuze ongedaan maken (backtracken, overeenkomstig de gestippelde pijlen). Om dat te doen, verwijderen we het laatste token terug uit de token-sequentie, en moeten we zorgen dat we terug de niet-ingekorte string gebruiken. We proberen dan opnieuw met een ander token.

Hoe ziet dat eruit in code? Zo:

private static List<String> findAny(String remainingString,
                                    List<String> allTokens,
                                    List<String> usedTokens) {
    // basisgeval
    if (remainingString.isEmpty()) return usedTokens;

    for (String tok : allTokens) {
        // probeer token tok
        if (remainingString.startsWith(tok)) {
            // uitbreiden gedeeltelijke oplossing
            usedTokens.add(tok); 
            var shorterString = remainingString.substring(tok.length());
            // recursief verder zoeken
            var solution = findAny(shorterString, allTokens, usedTokens);
            if (solution != null) {
                return solution;
            } else {
                // ongedaan maken
                usedTokens.removeLast();
            }
        }
    }
    return null;
}

De gedeeltelijke oplossing wordt voorgesteld met de twee parameters remainingString en usedTokens. Het basisgeval komt overeen met een lege string; we hebben dan een oplossing gevonden. Die oplossing zit in de parameter usedTokens.

Als de string niet leeg is, proberen we alle tokens beurt om de beurt uit.

Als een token niet overeenkomt met het begin van de string, kunnen we die token meteen overslaan.
Als die wel overeenkomt met het begin, voegen we de token toe aan de lijst met gebruikte keuzes en korten we de string in door de token vooraan te verwijderen. We zoeken vervolgens recursief verder naar een oplossing. Als we een oplossing vinden, hebben we meteen ook een oplossing voor het hele probleem. Zo niet, dan verwijderen we onze token terug uit de lijst van gebruikte tokens, vooraleer we opnieuw proberen met de volgende token. (De string hoeven we niet terug langer te maken; we kunnen gewoon remainingString blijven gebruiken)

Als we alle tokens geprobeerd hebben zonder een oplossing te vinden (return solution werd nooit uitgevoerd), dan is er geen oplossing en geven we null terug.

Om deze methode wat eenvoudiger bruikbaar te maken, kunnen we het worker-wrapper patroon toepassen. We voegen dan een tweede findAny-methode toe, die geen lijst van gebruikte tokens bevat, en de methode hierboven oproept met een lege lijst.

public static List<String> findAny(String string, List<String> tokens) {
    return findAny(string, tokens, new ArrayList<>());
}

public static void main(String[] args) {
    // voorbeeld van gebruik
    System.out.println(findAny("catsanddogs", 
                               List.of("s", "an", "ca", "cat", "dog", "and", "sand", "dogs")));
}

Skelet-programma (algemeen)

Backtracking-algoritmes volgen vaak een gelijkaardige structuur. Naast een voorbeeld geven we daarom telkens ook een skelet-programma: een algemene structuur die je vaak kan herbruiken. Backtracking-algoritmes draaien allemaal rond het gebruik van een partiële oplossing: dat is de sequentie van keuzes die je reeds gemaakt hebt, en de toestand waarin je je daardoor bevindt. Voor elk probleem zal je een geschikte representatie (datastructuur) moeten kiezen voor je partiële oplossing. Om de skelet-programma’s algemeen te houden, gebruiken we hiervoor volgende interfaces (het zal later duidelijk worden waarvoor de verschillende methodes precies dienen):

interface PartialSolution {
    boolean isComplete();  // volledige oplossing?
    boolean shouldAbort(); // leidt sowieso niet tot oplossing?
    Collection<Extension> extensions(); // mogelijke keuzes/extensies
    Solution toSolution(); // zet om naar finale oplossing
    boolean canImproveUpon(Solution solution); // vergelijken van oplossingen
}

public interface Extension {
    void apply(PartialSolution solution); // pas keuze toe op partiële oplossing
    void undo(PartialSolution solution);  // maak keuze ongedaan
}

interface Solution {
    boolean isBetterThan(Solution other); // vergelijken van oplossingen
}

In de algoritmes die je zelf schrijft zal je natuurlijk niet exact deze interfaces gebruiken, maar kan je zelf kiezen hoe je de oplossingen best voorstelt. Maar zelfs zonder deze interfaces te gebruiken is het vaak wel nuttig om eens na te denken over hoe je de operaties uit de interfaces kan uitvoeren met jouw voorstelling.

Skelet-programma: een willekeurige oplossing zoeken

Onderstaande code geeft het skelet om eender welke oplossing voor het probleem te vinden. We maken gebruik van het worker-wrapper patroon. Het eigenlijke werk gebeurt in de recursieve findAnySolution-methode. Die zoekt een oplossing voor het hele probleem, vertrekkend van een gegeven partiële oplossing.

We gaan eerst na of de huidige partiële oplossing toevallig al een oplossing is voor het hele probleem (hier via de isComplete()-methode). Dit is het basisgeval voor de recursie. Als dat zo is, moeten we niet verder zoeken, en geven we de oplossing terug. Soms moeten we nog enkele bewerkingen doen om de partiële oplossing om te zetten in het verwachte formaat van de oplossing. Dat wordt hier aangeduid met de toSolution()-methode.
Soms kan je op voorhand al snel zien dat een partiële oplossing nooit tot een oplossing kan leiden (shouldAbort()). Dan geven we meteen op, en geven we null terug (geen oplossing).
In alle andere gevallen overlopen we elke mogelijke uitbreiding (keuze) van de partiële oplossing (gegenereerd met extensions()). We veranderen de partiële oplossing door elk van de uitbreidingen (één voor één) toe te passen (apply()). Dan zoeken we recursief naar een volledige oplossing, vertrekkend van die uitgebreide partiële oplossing. Zodra we zo een (volledige) oplossing bekomen, geven we die terug. Als een uitbreiding niet tot een oplossing leidt, maken we ze ongedaan (undo()) en proberen we de volgende uitbreiding.
Als we alle mogelijke uitbreidingen overlopen hebben, en geen oplossing gevonden hebben, geven we op. We geven null terug.

public Solution solve() {
    PartialSolution initial = createInitialSolution();
    return findAnySolution(initial);
}

private Solution findAnySolution(PartialSolution current) {
    if (current.isComplete()) return current.toSolution();
    if (current.shouldAbort()) return null;
    for (var extension : current.extensions()) {
        extension.apply(current);
        var solution = findAnySolution(current);
        if (solution != null) {
            return solution;
        } else {
            extension.undo(current);
        }
    }
    return null;
}

Vergelijk

Vergelijk deze skelet-code met de code voor het token segmentatie voorbeeld. Herken je de verschillende onderdelen?

private static List<String> findAny(String remainingString,
                                    List<String> allTokens,
                                    List<String> usedTokens) {
    // if (current.isComplete()) return current.toSolution();
    if (remainingString.isEmpty()) return usedTokens;

    // if (current.shouldAbort()) return null;

    // for (var extension : current.extensions()) {
    for (String tok : allTokens) {
        if (remainingString.startsWith(tok)) {
            // extension.apply(current);
            usedTokens.add(tok); 
            var shorterString = remainingString.substring(tok.length());
            // var solution = findAnySolution(current);
            var solution = findAny(shorterString, allTokens, usedTokens);
            if (solution != null) {
                return solution;
            } else {
                // extension.undo(current);
                usedTokens.removeLast();
            }
        }
    }
    return null;
}

(Onze code voor token segmentatie bevat geen code die overeenkomt met shouldAbort.)

Alle oplossingen zoeken

Een variant van het zoeken van één oplossing is het zoeken van alle oplossingen. Om dat te doen, doen we in essentie hetzelfde als bij het zoeken van één oplossing. Nadat we een oplossing gevonden hebben, stoppen we echter niet: we houden de gevonden oplossing bij en gaan (met backtracking) verder op zoek naar eventuele andere oplossingen.

Voorbeeld: token segmentatie

Stel: we willen niet één, maar alle mogelijke segmentaties zoeken. We kunnen vertrekken van de versie om één oplossing te zoeken, maar moeten dan enkele wijzigingen doorvoeren.

Een eerste duidelijke wijziging is het terugkeertype. In plaats van één lijst van tokens, moeten we nu meerdere lijsten van tokens kunnen teruggeven. We kiezen daarom voor List<List<String>> als terugkeertype.

Een tweede wijziging komt voort vanuit het volgende inzicht. Waar we bij het zoeken van 1 oplossing meteen konden stoppen eens we een oplossing gevonden hadden, zullen we bij het zoeken naar alle oplossingen verder moeten backtracken nadat we een oplossing tegengekomen zijn. Dat betekent dat, op het moment dat we een oplossing vinden, we die ergens willen ‘wegschrijven’. We voegen daarom een extra parameter toe, een lijst foundSoFar, die alle oplossingen voorstelt die we eerder al gevonden hebben. Telkens we een nieuwe oplossing tegenkomen, voegen we die toe aan foundSoFar. Nadat we (via backtracking) alle keuzes doorlopen hebben, bevat foundSoFar alle gevonden oplossingen.

Een derde wijziging is dat we geen null meer teruggeven als we geen oplossing vinden; als er geen oplossingen zijn voor het probleem, vertaalt zich dat in een lege lijst van oplossingen.

In code:

public static List<List<String>> findAll(String string, List<String> tokens) {
    return findAll(string, tokens, new ArrayList<>(), new ArrayList<>());
}

private static List<List<String>> findAll(String remainingString,
                                          List<String> allTokens,
                                          List<String> usedTokens,
                                          List<List<String>> foundSoFar) {
    if (remainingString.isEmpty()) {
        foundSoFar.add(List.copyOf(usedTokens));
        return foundSoFar;
    };

    for (String tok : allTokens) {
        if (remainingString.startsWith(tok)) {
            usedTokens.add(tok);
            var shorterString = remainingString.substring(tok.length());
            findAll(shorterString, allTokens, usedTokens, foundSoFar);
            usedTokens.removeLast();
        }
    }
    return foundSoFar;
}

Belangrijk om op te merken is dat we de lijst usedTokens kopiëren wanneer we die toevoegen aan de lijst foundSoFar. Dat is noodzakelijk: de usedTokens-lijst is immers deel van de partiële oplossing, en die lijst zal later nog aangepast (bijvoorbeeld met .removeLast()) wanneer we verder naar oplossingen zoeken. In het vorige voorbeeld was dit niet essentieel; zodra we een oplossing vonden, gaven we de gevonden lijst meteen terug en stopten we met zoeken.

In de uitvoeringsboom voor het zoeken van alle oplossingen zien we dat alle mogelijkheden overlopen en teruggegeven worden. Alle groene knopen zijn oplossingen, en zullen (van links naar rechts) aan de lijst foundSoFar toegevoegd worden.

graph TB

start["[], catsanddogs"]
start -->|ca| ca
ca["[ca], tsanddogs"]
class ca fail
start -->|cat| cat
cat["[cat], sanddogs"]
cat -->|s| cat_s
cat_s["[cat, s], anddogs"]
cat_s -->|an| cat_s_an
cat_s_an["[cat, s, an], ddogs"]
class cat_s_an fail
cat_s -->|and| cat_s_and
cat_s_and["[cat, s, and], dogs"]
cat_s_and -->|dog| cat_s_and_dog
cat_s_and_dog["[cat, s, and, dog], s"]
cat_s_and_dog -->|s| cat_s_and_dog_s
cat_s_and_dog_s["[cat, s, and, dog, s], "]
class cat_s_and_dog_s success
cat_s_and -->|dogs| cat_s_and_dogs
cat_s_and_dogs["[cat, s, and, dogs], "]
class cat_s_and_dogs success
cat -->|sand| cat_sand
cat_sand["[cat, sand], dogs"]
cat_sand -->|dog| cat_sand_dog
cat_sand_dog["[cat, sand, dog], s"]
cat_sand_dog -->|s| cat_sand_dog_s
cat_sand_dog_s["[cat, sand, dog, s], "]
class cat_sand_dog_s success
cat_sand -->|dogs| cat_sand_dogs
cat_sand_dogs["[cat, sand, dogs], "]
class cat_sand_dogs success

classDef success fill:#2c2,stroke:#393,stroke-width:3,color:white;
classDef fail fill:#c22,stroke:#933,stroke-width:3,color:white;

Dit duurt uiteraard een stuk langer dan enkel de eerste oplossing teruggeven. We doorlopen immers steeds alle mogelijkheden.

Skelet-programma: alle oplossingen zoeken

We geven opnieuw een skelet-programma, dit keer om alle oplossingen voor het probleem te vinden.

Het eigenlijke werk gebeurt in de recursieve findAllSolutions-methode. Die doet grotendeels hetzelfde als de findAnySolution-methode uit het skelet-programma voor één oplossing. Het verschil is dat er nu een extra parameter is, namelijk een collectie van alle tot dan toe gevonden (volledige) oplossingen, solutionsSoFar. Elke keer een nieuwe oplossing gevonden wordt, voegen we die toe aan solutionsSoFar. De extra parameter wordt geïnitialiseerd in solve met een lege lijst.

public Collection<Solution> solve() {
    PartialSolution initial = createInitialSolution();
    return findAllSolutions(initial, new ArrayList<>());
}

private Collection<Solution> findAllSolutions(PartialSolution current, Collection<Solution> solutionsSoFar) {
    if (current.isComplete()) {
        solutionsSoFar.add(current.toSolution());
        return solutionsSoFar;
    }
    if (current.shouldAbort()) return solutionsSoFar;
    for (var extension : current.extensions()) {
        extension.apply(current);
        findAllSolutions(current, solutionsSoFar);
        extension.undo(current);
    }
    return solutionsSoFar;
}

Vergelijk

Vergelijk deze skelet-code opnieuw met de code voor het token segmentatie voorbeeld. Herken je de verschillende onderdelen?

private static List<List<String>> findAll(String remainingString,
                                          List<String> allTokens,
                                          List<String> usedTokens,
                                          List<List<String>> foundSoFar) {
    // if (current.isComplete()) {
    if (remainingString.isEmpty()) {
        // solutionsSoFar.add(current.toSolution());
        foundSoFar.add(List.copyOf(usedTokens));
        // return solutionsSoFar;
        return foundSoFar;
    };

    // if (current.shouldAbort()) return solutionsSoFar;

    // for (var extension : current.extensions()) {
    for (String tok : allTokens) {
        if (remainingString.startsWith(tok)) {
            // extension.apply(current);
            usedTokens.add(tok);
            var shorterString = remainingString.substring(tok.length());
            // findAllSolutions(current, solutionsSoFar);
            findAll(shorterString, allTokens, usedTokens, foundSoFar);
            // extension.undo(current);
            usedTokens.removeLast();
        }
    }
    // return solutionsSoFar;
    return foundSoFar;
}

Een optimale oplossing zoeken

De laatste variant die we beschouwen is het zoeken van een optimale oplossing voor een probleem. Je zou dat kunnen doen door eerst alle oplossingen te zoeken, en dan in die lijst van oplossingen de meest optimale oplossing te zoeken. Het bijhouden van alle oplossingen kan in sommige gevallen echter leiden tot een te hoog geheugengebruik. In plaats van alle oplossingen bij te houden, is het daarom beter om enkel de (tot dantoe) beste oplossing te bewaren.

Het zoeken van een optimale oplossing duurt dus meestal even lang als het zoeken van alle oplossingen, maar niet altijd. Soms is het zinloos om nog naar oplossingen te blijven zoeken die sowieso nooit beter kunnen zijn dan een reeds eerder gevonden oplossing. Je kan immers meteen stoppen met zoeken wanneer je weet dat de huidige partiële oplossing nooit meer tot een betere finale oplossing kan leiden dan de tot dan toe beste oplossing. Dat kan een hoop werk besparen, en de tijd gevoelig inkorten.

Voorbeeld: token segmentatie

De optimale oplossing wordt gedefinieerd als de oplossing die de string splitst in het minst aantal tokens.

De wijzigingen ten opzichte van het algoritme om alle oplossingen te zoeken zijn devolgende:

Ten eerste hoeven we geen lijst van oplossingen meer bij te houden, maar enkel de tot dan toe beste oplossing. Dat doen we in een variabele bestSoFar. Die variabele is null wanneer er nog geen oplossing gevonden werd (bijvoorbeeld bij de start van de zoektocht).
Ten tweede moeten we, wanneer we een oplossing gevonden hebben, nagaan of die beter is dan de vorige beste oplossing (als die er is). Aangezien we zoeken naar de splitsing met het minst aantal tokens, vergelijken we op basis van de lengte van de oplossing. We geven de kortste van de twee terug.
Tenslotte kijken we of we de zoektocht voortijdig kunnen staken. Wanneer de huidige splitsing al meer tokens bevat dan de beste splitsing die we op dat moment kennen, heeft het geen zin om nog verder te zoeken. Er kunnen immers enkel tokens bijkomen.

Zoek deze wijzigingen in onderstaande code:

public static List<String> findShortest(String string, List<String> tokens) {
    return findShortest(string, tokens, new ArrayList<>(), null);
}

private static List<String> findShortest(String remainingString,
                                         List<String> allTokens,
                                         List<String> usedTokens,
                                         List<String> bestSoFar) { // 1. 
    if (remainingString.isEmpty()) {
        var solution = List.copyOf(usedTokens);
        // 2.
        if (bestSoFar == null || solution.size() < bestSoFar.size()) {
            return solution;
        } else {
            return bestSoFar;
        }
    };

    // 3.
    if (bestSoFar != null && bestSoFar.size() <= usedTokens.size()) {
        return bestSoFar;
    }

    for (String tok : allTokens) {
        if (remainingString.startsWith(tok)) {
            usedTokens.add(tok);
            var shorterString = remainingString.substring(tok.length());
            bestSoFar = findShortest(shorterString, allTokens, usedTokens, bestSoFar);
            usedTokens.removeLast();
        }
    }
    return bestSoFar;
}

Merk op dat we na de recursieve oproep ook de variabele bestSoFar aanpassen, voor het geval de recursieve oproep een betere oplossing gevonden heeft.

De uitvoeringsboom ziet er als volgt uit. De gele knopen zijn oplossingen die op een bepaald moment de beste oplossing waren, maar later vervangen zijn door een nog betere oplossing.

graph TB

start["[], catsanddogs"]
start -->|ca| ca
ca["[ca], tsanddogs"]
class ca fail
start -->|cat| cat
cat["[cat], sanddogs"]
cat -->|s| cat_s
cat_s["[cat, s], anddogs"]
cat_s -->|an| cat_s_an
cat_s_an["[cat, s, an], ddogs"]
class cat_s_an fail
cat_s -->|and| cat_s_and
cat_s_and["[cat, s, and], dogs"]
cat_s_and -->|dog| cat_s_and_dog
cat_s_and_dog["[cat, s, and, dog], s"]
cat_s_and_dog -->|s| cat_s_and_dog_s
cat_s_and_dog_s["[cat, s, and, dog, s], "]
class cat_s_and_dog_s bestsofar
cat_s_and -->|dogs| cat_s_and_dogs
cat_s_and_dogs["[cat, s, and, dogs], "]
class cat_s_and_dogs bestsofar
cat -->|sand| cat_sand
cat_sand["[cat, sand], dogs"]
cat_sand -->|dog| cat_sand_dog
cat_sand_dog["[cat, sand, dog], s"]
cat_sand_dog -->|s| cat_sand_dog_s
cat_sand_dog_s["[cat, sand, dog, s], "]
cat_sand -->|dogs| cat_sand_dogs
cat_sand_dogs["[cat, sand, dogs], "]

class cat_sand_dogs success

classDef success fill:#2c2,stroke:#393,stroke-width:3,color:white;
classDef bestsofar fill:#cc2,stroke:#993,stroke-width:3,color:black;
classDef fail fill:#c22,stroke:#933,stroke-width:3,color:white;

Skelet-programma: optimale oplossing

Ook het zoeken naar een optimale oplossing via backtracking heeft vaak dezelfde vorm. We bespreken daarom een derde skelet-programma.

Het eigenlijke werk gebeurt opnieuw in de recursieve findOptimalSolution-methode. Die doet grotendeels hetzelfde als bij het programma om één of alle oplossingen te zoeken. Het speciale hier is een extra parameter, namelijk de beste tot dan toe gevonden (volledige) oplossing bestSoFar. Elke keer een nieuwe oplossing gevonden wordt, vergelijken we die met de beste tot dan toe (via isBetterThan), en geven de betere van de twee terug. De extra parameter wordt geïnitialiseerd in solve met null: er is nog geen oplossing om mee te vergelijken.

Merk op dat we dus niet eerst alle oplossingen zoeken en bijhouden om daarna de beste te selecteren; we houden enkel de beste oplossing tot dan toe bij en vergelijken daarmee.

Daarenboven voegen we nog een optimalisatie toe: als we op een bepaald moment merken dat de huidige partiële oplossing nooit meer kan uitgroeien tot een oplossing die beter is dan de beste reeds gekende oplossing, dan stoppen we met zoeken op basis van die partiële oplossing. Bijvoorbeeld, wanneer we een kortste pad zoeken in een doolhof en het huidige pad (waarmee we nog niet uit het doolhof zijn) is al langer dan het tot dan toe beste pad (dat wel reeds heel het doolhof oploste), dan hoeven we niet meer verder te zoeken: extra stappen toevoegen zal immers nooit kunnen leiden tot een korter pad. We modelleren dit met de canImproveUpon-methode.

public Solution solve() {
    PartialSolution initial = createInitialSolution();
    return findOptimalSolution(initial, null);
}

private Solution findOptimalSolution(PartialSolution current, Solution bestSoFar) {
    if (current.isComplete()) {
        var solution = current.toSolution();
        if (bestSoFar == null || solution.isBetterThan(bestSoFar)) {
            return solution;
        } else {
            return bestSoFar;
        }
    }
    if (current.shouldAbort() ||
            (bestSoFar != null && !current.canImproveUpon(bestSoFar))) {
        return bestSoFar;
    }
    for (var extension : current.extensions()) {
        extension.apply(current);
        bestSoFar = findOptimalSolution(current, bestSoFar);
        extension.undo(current);
    }
    return bestSoFar;
}

Vergelijk

Vergelijk deze skelet-code opnieuw met de code voor het token segmentatie voorbeeld. Herken je de verschillende onderdelen?

private static List<String> findShortest(String remainingString,
                                         List<String> allTokens,
                                         List<String> usedTokens,
                                         List<String> bestSoFar) {
    // if (current.isComplete()) {
    if (remainingString.isEmpty()) {
        // var solution = current.toSolution();
        var solution = List.copyOf(usedTokens);
        // if (bestSoFar == null || solution.isBetterThan(bestSoFar)) {
        if (bestSoFar == null || solution.size() < bestSoFar.size()) {
            return solution;
        } else {
            return bestSoFar;
        }
    };

    // if (current.shouldAbort() ||
    //      (bestSoFar != null && !current.canImproveUpon(bestSoFar))) {
    if (bestSoFar != null && bestSoFar.size() <= usedTokens.size()) {
        return bestSoFar;
    }

    // for (var extension : current.extensions()) {
    for (String tok : allTokens) {
        if (remainingString.startsWith(tok)) {
            // extension.apply(current);
            usedTokens.add(tok);
            var shorterString = remainingString.substring(tok.length());
            // bestSoFar = findOptimalSolution(current, bestSoFar);
            bestSoFar = findShortest(shorterString, allTokens, usedTokens, bestSoFar);
            // extension.undo(current);
            usedTokens.removeLast();
        }
    }
    return bestSoFar;
}

Efficiëntie van backtracking

Backtracking is vaak niet heel efficiënt. Bijvoorbeeld, als er $ k $ keuzepunten zijn, en je bij elke keuzepunt precies $ m$ mogelijkheden hebt, dan zijn er in totaal $ m^k $ mogelijke paden die je moet proberen. Door snel te herkennen wanneer een partiële oplossing niet zal leiden tot een geschikte oplossing, en de zoekoperatie dan onmiddellijk af te breken, kan je het algoritme soms wel een pak efficiënter maken.

Kopiëren vs. aanpassen en herstellen

In de skeletten hierboven maakten we steeds gebruik van apply() en undo(): we passen de partiële oplossing aan (door ze uit te breiden), en maken die aanpassing later weer ongedaan. Dat gaat makkelijk als de aanpassing eenvoudig ongedaan te maken is, bijvoorbeeld een element toevoegen aan een lijst en dat nadien weer verwijderen.

Als het ongedaan maken niet zo eenvoudig is (bijvoorbeeld omdat er na de aanpassing heel wat herberekend wordt), is het vaak eenvoudiger om de volledige toestand eerst te kopiëren en verder te werken met deze kopie. Dat heeft als nadeel een hoger geheugengebruik, maar vereenvoudigt het uitbreiden en herstellen van de partiële oplossing wel aanzienlijk. Je hoeft immers niets ongedaan te maken; aangezien alle aanpassingen op een kopie gebeurd zijn, kan je gewoon teruggrijpen naar de originele toestand. Die is ongewijzigd, aangezien alle aanpassingen op een kopie gebeurden.

Hieronder zie je een voorbeeld hiervan (een variant om één oplossing te zoeken voor het token segmentatie probleem). De commentaarregels geven aan wat er van belang is.

private static List<String> findAny(String remainingString,
                                    List<String> allTokens,
                                    List<String> usedTokens) {
    if (remainingString.isEmpty()) return usedTokens;

    for (String tok : allTokens) {
        if (remainingString.startsWith(tok)) {
            // uitbreiding gedeeltelijke oplossing OP EEN KOPIE
            var copyOfUsedTokens = new ArrayList<>(usedTokens);
            copyOfUsedTokens.add(tok); 
            var shorterString = remainingString.substring(tok.length());
            // recursief verder zoeken OP BASIS VAN DE KOPIE
            var solution = findAny(shorterString, allTokens, copyOfUsedTokens);
            if (solution != null) {
                return solution;
            } else {
                // we hoeven hier NIETS ongedaan te maken,
                // de volgende iteratie gebruikt opnieuw de originele usedTokens-lijst
            }
        }
    }
    return null;
}

Backtracking: oefeningen

Variant op token-segmentatie

In het voorbeeld van token-segmentatie mocht een token meermaals gebruikt worden. Schrijf nu een algoritme dat uitzoekt of een token gesegmenteerd kan worden op een manier waarbij elke token hoogstens één keer gebruikt wordt. Doe dat voor de drie varianten:

één oplossing
alle oplossingen
optimale oplossing

8-queens / n-queens

Dit is de klassieker onder de backtracking-algoritmes. Schrijf een backtracking-algoritme om te zoeken hoe je, op een schaakbord van 8x8 vakjes, 8 koninginnen kan plaatsen zodat ze elkaar niet kunnen slaan.

Voor wie niet thuis is in schaken: een koningin (queen, ‘Q’) kan elke andere koningin slaan die zich in dezelfde rij, kolom, of diagonaal bevindt:

Uitbreiding 1: Doe dit voor een schaakbord van willekeurige grootte n, in plaats van 8.

Uitbreiding 2: Zoek alle oplossingen in plaats van 1 oplossing (voor een bord van 5x5).

Knight’s tour

Nog een klassieker met een schaakbord. Schrijf een backtracking-algoritme om met een paard, beginnend op positie (0, 0), precies één keer op elk vakje van het bord te komen.

Een paard (knight, ‘N’) beweegt 2 vakjes in een richting, en 1 vakje in de orthogonale richting:

Hint als je oplossing te lang duurt: Begin met een kleiner bord (5x5), en overloop de mogelijke volgende posities van het paard steeds volgens de wijzers van de klok.

Uitbreiding: Zoek alle oplossingen in plaats van 1 oplossing, voor een klein bord (5x5). Zoek ook online op hoeveel oplossingen er bestaan voor een 8x8 bord.

SEND+MORE=MONEY

Schrijf een backtracking-algoritme om een letterpuzzel op te lossen zodanig dat de som klopt.

Elke letter komt in de hele puzzel overeen met hetzelfde cijfer (0–9).
Twee verschillende letters staan altijd voor verschillende cijfers.
De getallen beginnen niet met 0 (geen leading zeros).

Bijvoorbeeld:

    S E N D
+   M O R E
-----------
  M O N E Y

ONE + TWO = SIX
SUN + FUN = SWIM
CRACK + HACK = ERROR
MATH + MYTH = HARD
BASE + BALL = GAMES

Hint: onderstaande hulpfuncties kunnen misschien handig zijn. Ook Integer.parseInt(String s) om een String om te zetten naar een int kan nuttig zijn.

private static String replaceCharWithNumber(String str, char charToReplace, int digit) {
    return str.replace(charToReplace, (char) ('0' + digit));
}

private static boolean containsLetter(String str) {
    return str.chars().anyMatch(Character::isLetter);
}

Uitbreiding: Laat toe om meer dan twee termen op te tellen, bijvoorbeeld ONE + TWO + SIX = NINE.

Uitbreiding: Zoek alle oplossingen.

Uurrooster planner

Schrijf een programma om een conflict-vrije uurrooster te maken voor een lijst van vakken. Bij elk vak hoort een verzameling van personen (bv. leerkracht en studenten). We vereenvoudigen het uurrooster tot een verzameling van vaste slots waarop vakken ingepland kunnen worden. Elk slot stellen we voor door een positief getal. Zo kan slot 1 bijvoorbeeld staan voor maandagmorgen om 8u30, slot 2 voor maandagmorgen om 10u30, etc.

Enkele beperkingen waaraan het rooster moet voldoen:

(optimaal) Het uiteindelijke uurrooster moet gebruik maken van zo weinig mogelijk slots.
(conflict-vrij) Een persoon mag nooit voor 2 verschillende vakken in hetzelfde slot ingeroosterd worden.
(capaciteitsconform) Er mogen nooit meer dan 5 vakken op hetzelfde slot ingepland worden, zodat er steeds voldoende lokalen zijn.

Woorden samentrekken

Maak een methode die de kortste samentrekking zoekt van een gegeven verzameling van woorden. We spreken van een samentrekking wanneer het einde van een woord overeenkomt met het begin van het woord dat daarop volgt (minstens 1 overlappende letter). Bijvoorbeeld: banaananas is een samentrekking van ananas en banaan, waar we beginnen met het woord banaan, en de letters an overlappen.

Voor de woorden "besturend", "declaratiesysteem", "deelgemeente", "gemeentebesturen", "merendeel", "programmeren", "sturende", "urendeclaraties" bekom je als kortste samentrekking "programmerendeelgemeentebesturendeclaratiesysteem".
Voor [samentrekking, trekkingsdata, datavoorziening, voorzieningsfonds, fondsmanager, managersfuncties, functiesysteem, systeemdata] wordt dat samentrekkingsdatavoorzieningsfondsmanagersfunctiesysteemdata.

Soms bestaat er geen samentrekking.

Uitbreiding: Zoek ook de langste samentrekking. Voor het eerste voorbeeld hierboven is dat programmerendeelgemeentebesturendeclaratiesturendeclaratiesysteem. Voor het tweede functiesysteemdatavoorzieningsfondsmanagersfunctiesamentrekkingsdata.

Traveling sales person

Gegeven een lijst van plaatsen met bijhorende (x, y)-coördinaten en een startplaats, zoek de kortste tour (dus met de kleinste totale afgelegde afstand) die terug uitkomt op de startplaats en onderweg elke gegeven plaats exact één keer bezoekt.

private static Route shortestRoute(Location start, List<Location> otherLocations) { ... }

Bijvoorbeeld, voor de volgende lijst van locaties (hieronder visueel weergegeven) heeft de kortste tour vertrekkend en eindigend bij A een lengte 3.7485395:

"A",	0,   0
"L0",	0.723174203,	0.990898897
"L1",	0.253293106,	0.60880037
"L2",	0.805869514,	0.875412785
"L3",	0.716048511,	0.071917022
"L4",	0.796260972,	0.578716937
"L5",	0.908125618,	0.148914579
"L6",	0.975219897,	0.06559603
"L7",	0.069517882,	0.090752294
"L8",	0.424466728,	0.874391044
"L9",	0.575103864,	0.39649687
"L10",	0.25831525,	0.152792153
"L11",	0.26042993,	0.461681947
"L12",	0.439100791,	0.211405433
"L13",	0.614212143,	0.033457912
"L14",	0.688896121,	0.6841128

Uitbreiding: Alle volgordes van locaties proberen leidt tot enorm veel mogelijkheden (hoeveel?), en dus een zeer traag algoritme. Bedenk één of meer opties om de zoektocht wat te versnellen (al zal het algoritme traag blijven voor veel coördinaten; hoop niet op een oplossing die voldoende snel werkt voor meer dan een 20-tal locaties).

Doolhof

Schrijf een functie om het kortste pad door een doolhof te vinden van het begin- naar een eindpunt. Een doolhof wordt voorgesteld als een string, met

@ voor het startpunt (steeds exact één per doolhof)
$ voor een eindpunt (minstens één per doolhof)
. voor een vrije cel (hier kan je doorgaan)
X voor een cel met een muur (hier kan je niet doorheen gaan)

Je kan je enkel horizontaal of verticaal verplaatsen naar een naburige vrije cel.

Bijvoorbeeld:

@..X.....X
X.XXX.X.X.
..X.X.X...
.XX...XX.X
....XXX..$

Handdoeken

Maak de eerste opgave van dag 19 van de Advent of code 2024.

Snakefill

Oud-examenvraag

Dit is een oud-examenvraag.

In het spel SnakeFill beweeg je het hoofd van een slang over een bord in een bepaalde richting. Het bord bestaat uit vrije cellen en muren. De slang wordt steeds langer, en beweegt steeds verder in dezelfde richting tot die een obstakel (een muur, de rand van het bord, of een deel van zichzelf) tegenkomt. Pas dan kan je de richting veranderen. Het hoofd van de slang beweegt dus steeds van obstakel tot obstakel.

Het doel van het spel is om alle vakjes van het bord te vullen met de slang. Hieronder zie je een voorbeeld. Het hoofd van de slang begint (fig. A) linksboven op positie (0, 0), beweegt dan naar onder (B), dan naar rechts (C), etc. Helemaal rechts (fig. D) zie je een traject dat het hele bord vult. Dit komt overeen met de bewegingen [DOWN, RIGHT, UP, LEFT, UP, RIGHT, DOWN, RIGHT, UP, LEFT].

Ontwerp een backtracking-algoritme om, met zo weinig mogelijk bewegingen, het hele bord te vullen. Je geeft de oplossing terug als een lijst van bewegingen (Directions). Indien er geen oplossing is, geef je null terug. Je moet een solve-methode schrijven die opgeroepen wordt zoals getoond in de gegeven main-methode. In de solve-methode mag je gebruik maken van zelfgeschreven hulpmethodes.

Je krijgt alvast de interface van een Board-klasse om het bord van SnakeFill voor te stellen. Je mag ervan uitgaan dat er hiervan een implementatie beschikbaar is die correct werkt; je moet deze dus niet zelf schrijven. Er zijn ook hulpklassen gegeven om posities en richtingen voor te stellen. In principe volstaan de gegeven methodes in deze klassen om het probleem op te lossen. Je mag elk van deze klassen echter verder uitbreiden met extra methodes die je nuttig acht. Schrijf daarvoor de methode-hoofding en een beschrijving van wat de methode moet doen. Je hoeft de methode zelf niet te implementeren.

public interface Board {
  /* Huidige positie van het hoofd van de slang */
  Position getCurrentHead();
  /* Maakt de gegeven positie deel uit van het bord? */
  boolean isValid(Position pos);
  /* Is de gegeven positie vrij (geen muur, geen slang)” */
  boolean isFree(Position pos);
  /* Zijn alle posities van het bord gevuld? */
  boolean isFull();
  /* Telt het aantal opeenvolgende vrije cellen in de gegeven 
     richting vanaf het hoofd van de slang.
     In situatie (A) in het voorbeeld geeft deze methode
     5 terug voor DOWN, 2 voor RIGHT, en 0 voor LEFT en UP. */
  int freeCells(Direction dir);
  /* Maak de slang n vakken langer in de gegeven richting.
     In het voorbeeld ga je van (A) naar (B) met n=5 en dir=DOWN */
  void extendSnake(int n, Direction dir);
  /* Maak de slang n vakken korter in de gegeven richting.
     In het voorbeeld ga je van (B) naar (A) met n=5 en dir=UP  */
  void retractSnake(int n, Direction dir);
  /* Maak een kopie van het bord */
  Board copy();
}

/* Positie op het bord */
record Position(int row, int col) {
    /* Positie op n vakken vanaf de huidige positie in de 
       gegeven richting. */
    public Position go(Direction dir, int n) {
        return switch(dir) {
            case RIGHT -> new Position(row, col + n);
            case LEFT  -> new Position(row, col - n);
            case UP    -> new Position(row - n, col);
            case DOWN  -> new Position(row + n, col);
        };
    }
}

/* Een richting (UP, DOWN, LEFT, RIGHT). */
enum Direction {
    UP, DOWN, LEFT, RIGHT;
    public static final Direction[] ALL_DIRECTIONS = 
         {UP, DOWN, LEFT, RIGHT};
    …
    /* Geef de omgekeerde richting terug
       (UP <-> DOWN, LEFT <-> RIGHT) */
    public Direction opposite() { … };
}
 
public static void main(String[] args) {
  var board = … /* Maak een bord (dit hoef je niet te schrijven) */
  var solution = solve(board);
  if (solution != null)
    System.out.println(solution);
  else
    System.out.println("No solution");
}


public static List<Direction> solve(Board board) {
    // TODO
}

8. Recursie en backtracking

Subsections of 8. Recursie en backtracking

8.1 Recursie

Wat is recursie?

Recursie achter de schermen

Stack

Stack overflow

Eindigheid en invoergrootte

Recursief denken

Voorbeeld 1: grootste element

Voorbeeld 2: Toren van Hanoi

Recursie vs. iteratie

Efficiëntie

Patronen om het probleem te verkleinen

Recursie: oefeningen

Palindroom

String omkeren

Element zoeken in lijst

Duplicaten verwijderen

Greatest common divisor

Snelle macht

Sum of digits

Trap beklimmen

Gepast betalen

Gepast betalen (bis)

Alle prefixen van een String

Alle interleavings van twee strings

Vliegtuigreis

Powerset

Alle permutaties van een lijst berekenen

Gebalanceerde haakjes

Longest common subsequence

Boomstructuur

Stack omkeren

Toren van Hanoi (uitbreiding)

Sorteren van een lijst

reduce

8.2 Backtracking

Wat is backtracking?

Voorbeeld: token segmentatie

Eén (willekeurige) oplossing zoeken

Voorbeeld: token segmentatie

Skelet-programma (algemeen)

Skelet-programma: een willekeurige oplossing zoeken

Alle oplossingen zoeken

Voorbeeld: token segmentatie

Skelet-programma: alle oplossingen zoeken

Een optimale oplossing zoeken

Voorbeeld: token segmentatie

Skelet-programma: optimale oplossing

Efficiëntie van backtracking

Kopiëren vs. aanpassen en herstellen

Backtracking: oefeningen

Variant op token-segmentatie

8-queens / n-queens

Knight’s tour

SEND+MORE=MONEY

Uurrooster planner

Woorden samentrekken

Traveling sales person

Doolhof

Handdoeken

Snakefill