Backtracking: oefeningen
Variant op token-segmentatie
In het voorbeeld van token-segmentatie mocht een token meermaals gebruikt worden. Schrijf nu een algoritme dat uitzoekt of een token gesegmenteerd kan worden op een manier waarbij elke token hoogstens één keer gebruikt wordt. Doe dat voor de drie varianten:
- één oplossing
- alle oplossingen
- optimale oplossing
8-queens / n-queens
Dit is de klassieker onder de backtracking-algoritmes. Schrijf een backtracking-algoritme om te zoeken hoe je, op een schaakbord van 8x8 vakjes, 8 koninginnen kan plaatsen zodat ze elkaar niet kunnen slaan.
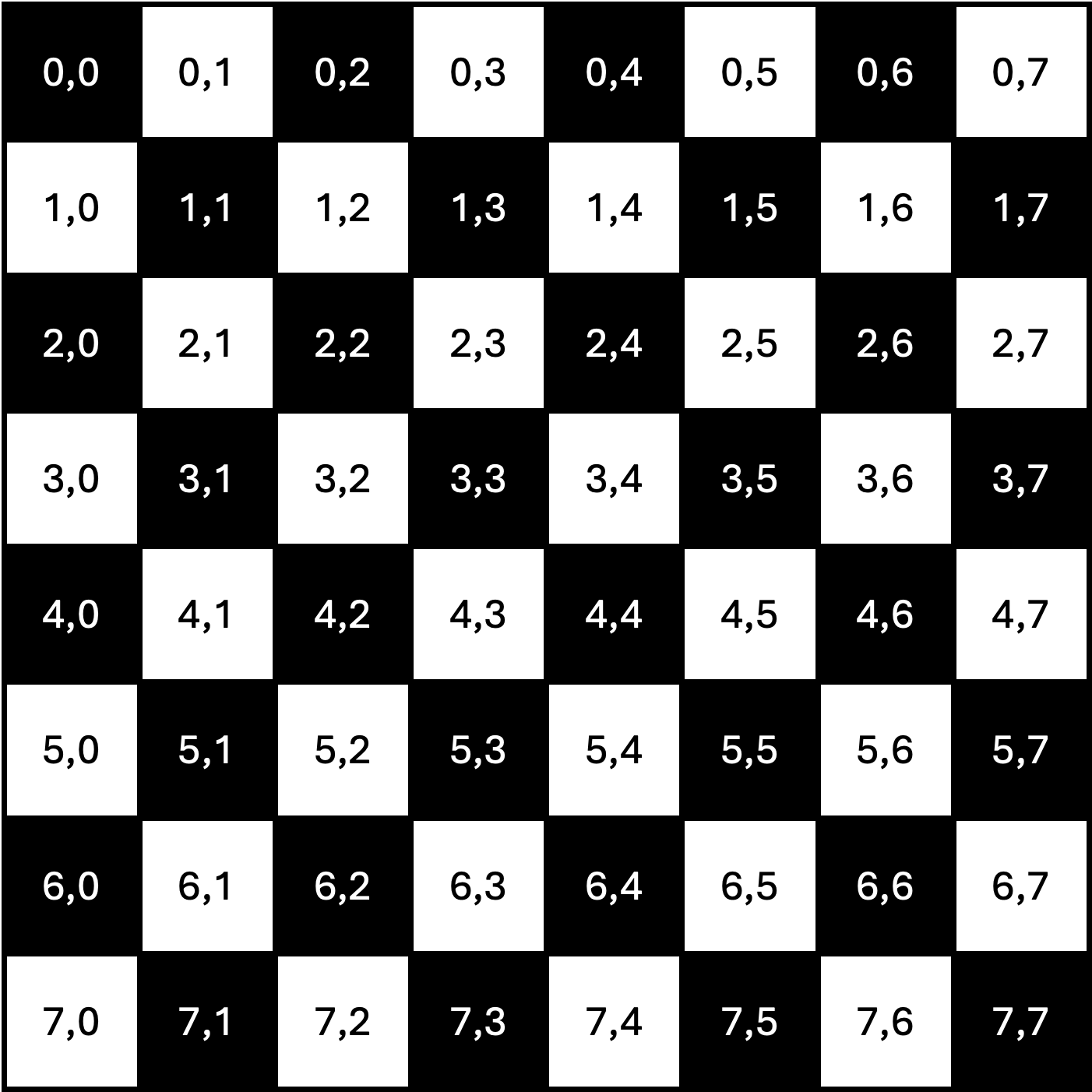
Voor wie niet thuis is in schaken: een koningin (queen, ‘Q’) kan elke andere koningin slaan die zich in dezelfde rij, kolom, of diagonaal bevindt:
Uitbreiding 1: Doe dit voor een schaakbord van willekeurige grootte n, in plaats van 8.
Uitbreiding 2: Zoek alle oplossingen in plaats van 1 oplossing (voor een bord van 5x5).
Knight’s tour
Nog een klassieker met een schaakbord. Schrijf een backtracking-algoritme om met een paard, beginnend op positie (0, 0), precies één keer op elk vakje van het bord te komen.
Een paard (knight, ‘N’) beweegt 2 vakjes in een richting, en 1 vakje in de orthogonale richting:
Hint als je oplossing te lang duurt: Begin met een kleiner bord (5x5), en overloop de mogelijke volgende posities van het paard steeds volgens de wijzers van de klok.
Uitbreiding: Zoek alle oplossingen in plaats van 1 oplossing, voor een klein bord (5x5). Zoek ook online op hoeveel oplossingen er bestaan voor een 8x8 bord.
SEND+MORE=MONEY
Schrijf een backtracking-algoritme om een letterpuzzel op te lossen zodanig dat de som klopt.
- Elke letter komt in de hele puzzel overeen met hetzelfde cijfer (0–9).
- Twee verschillende letters staan altijd voor verschillende cijfers.
- De getallen beginnen niet met 0 (geen leading zeros).
Bijvoorbeeld:
S E N D
+ M O R E
-----------
M O N E Yof
ONE + TWO = SIXSUN + FUN = SWIMCRACK + HACK = ERRORMATH + MYTH = HARDBASE + BALL = GAMES
Hint: onderstaande hulpfuncties kunnen misschien handig zijn. Ook Integer.parseInt(String s) om een String om te zetten naar een int kan nuttig zijn.
private static String replaceCharWithNumber(String str, char charToReplace, int digit) {
return str.replace(charToReplace, (char) ('0' + digit));
}
private static boolean containsLetter(String str) {
return str.chars().anyMatch(Character::isLetter);
}Uitbreiding: Laat toe om meer dan twee termen op te tellen, bijvoorbeeld ONE + TWO + SIX = NINE.
Uitbreiding: Zoek alle oplossingen.
Uurrooster planner
Schrijf een programma om een conflict-vrije uurrooster te maken voor een lijst van vakken. Bij elk vak hoort een verzameling van personen (bv. leerkracht en studenten). We vereenvoudigen het uurrooster tot een verzameling van vaste slots waarop vakken ingepland kunnen worden. Elk slot stellen we voor door een positief getal. Zo kan slot 1 bijvoorbeeld staan voor maandagmorgen om 8u30, slot 2 voor maandagmorgen om 10u30, etc.
Enkele beperkingen waaraan het rooster moet voldoen:
- (optimaal) Het uiteindelijke uurrooster moet gebruik maken van zo weinig mogelijk slots.
- (conflict-vrij) Een persoon mag nooit voor 2 verschillende vakken in hetzelfde slot ingeroosterd worden.
- (capaciteitsconform) Er mogen nooit meer dan 5 vakken op hetzelfde slot ingepland worden, zodat er steeds voldoende lokalen zijn.
Woorden samentrekken
Maak een methode die de kortste samentrekking zoekt van een gegeven verzameling van woorden.
We spreken van een samentrekking wanneer het einde van een woord overeenkomt met het begin van het woord dat daarop volgt (minstens 1 overlappende letter).
Bijvoorbeeld: banaananas is een samentrekking van ananas en banaan, waar we beginnen met het woord banaan, en de letters an overlappen.
Voor de woorden
"besturend", "declaratiesysteem", "deelgemeente", "gemeentebesturen", "merendeel", "programmeren", "sturende", "urendeclaraties"bekom je als kortste samentrekking"programmerendeelgemeentebesturendeclaratiesysteem".Voor
[samentrekking, trekkingsdata, datavoorziening, voorzieningsfonds, fondsmanager, managersfuncties, functiesysteem, systeemdata]wordt datsamentrekkingsdatavoorzieningsfondsmanagersfunctiesysteemdata.
Soms bestaat er geen samentrekking.
Uitbreiding: Zoek ook de langste samentrekking. Voor het eerste voorbeeld hierboven is dat programmerendeelgemeentebesturendeclaratiesturendeclaratiesysteem. Voor het tweede functiesysteemdatavoorzieningsfondsmanagersfunctiesamentrekkingsdata.
Traveling sales person
Gegeven een lijst van plaatsen met bijhorende (x, y)-coördinaten en een startplaats, zoek de kortste tour (dus met de kleinste totale afgelegde afstand) die terug uitkomt op de startplaats en onderweg elke gegeven plaats exact één keer bezoekt.
private static Route shortestRoute(Location start, List<Location> otherLocations) { ... }Bijvoorbeeld, voor de volgende lijst van locaties (hieronder visueel weergegeven) heeft de kortste tour vertrekkend en eindigend bij A een lengte 3.7485395:
"A", 0, 0
"L0", 0.723174203, 0.990898897
"L1", 0.253293106, 0.60880037
"L2", 0.805869514, 0.875412785
"L3", 0.716048511, 0.071917022
"L4", 0.796260972, 0.578716937
"L5", 0.908125618, 0.148914579
"L6", 0.975219897, 0.06559603
"L7", 0.069517882, 0.090752294
"L8", 0.424466728, 0.874391044
"L9", 0.575103864, 0.39649687
"L10", 0.25831525, 0.152792153
"L11", 0.26042993, 0.461681947
"L12", 0.439100791, 0.211405433
"L13", 0.614212143, 0.033457912
"L14", 0.688896121, 0.6841128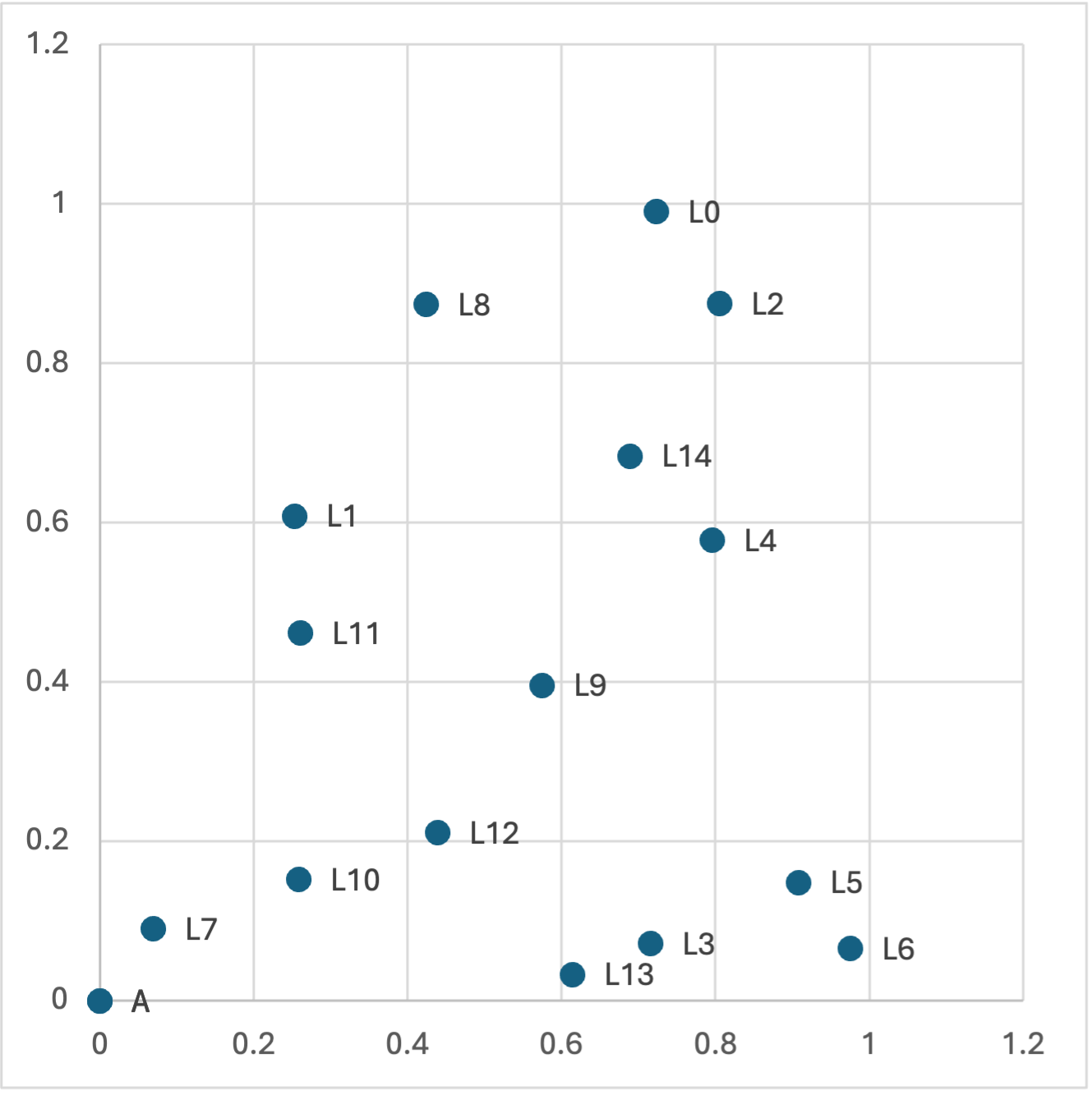
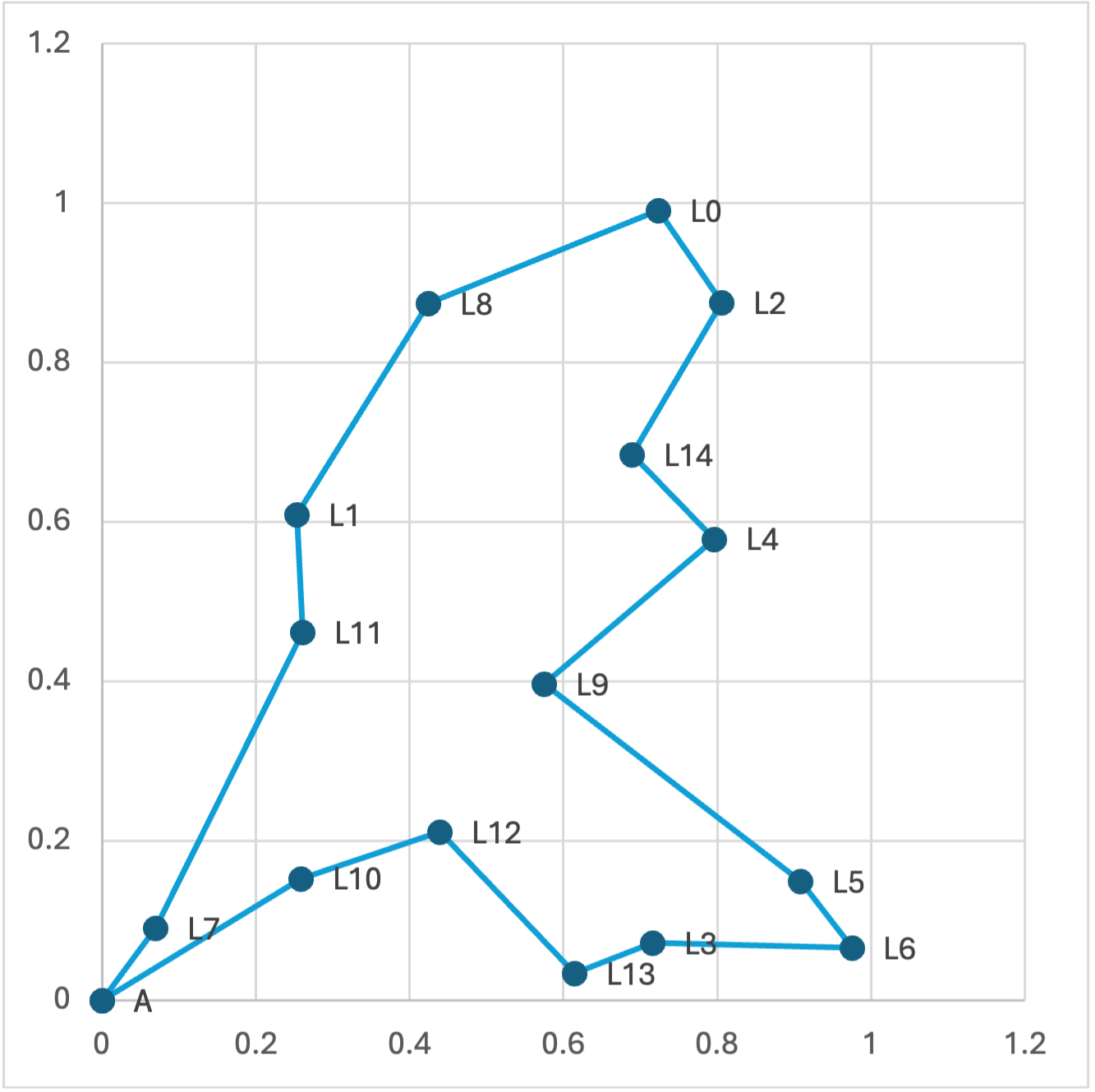
Uitbreiding: Alle volgordes van locaties proberen leidt tot enorm veel mogelijkheden (hoeveel?), en dus een zeer traag algoritme. Bedenk één of meer opties om de zoektocht wat te versnellen (al zal het algoritme traag blijven voor veel coördinaten; hoop niet op een oplossing die voldoende snel werkt voor meer dan een 20-tal locaties).
Doolhof
Schrijf een functie om het kortste pad door een doolhof te vinden van het begin- naar een eindpunt. Een doolhof wordt voorgesteld als een string, met
@voor het startpunt (steeds exact één per doolhof)$voor een eindpunt (minstens één per doolhof).voor een vrije cel (hier kan je doorgaan)Xvoor een cel met een muur (hier kan je niet doorheen gaan)
Je kan je enkel horizontaal of verticaal verplaatsen naar een naburige vrije cel.
Bijvoorbeeld:
@..X.....X
X.XXX.X.X.
..X.X.X...
.XX...XX.X
....XXX..$Handdoeken
Maak de eerste opgave van dag 19 van de Advent of code 2024.
Snakefill
Oud-examenvraag
Dit is een oud-examenvraag.
In het spel SnakeFill beweeg je het hoofd van een slang over een bord in een bepaalde richting. Het bord bestaat uit vrije cellen en muren. De slang wordt steeds langer, en beweegt steeds verder in dezelfde richting tot die een obstakel (een muur, de rand van het bord, of een deel van zichzelf) tegenkomt. Pas dan kan je de richting veranderen. Het hoofd van de slang beweegt dus steeds van obstakel tot obstakel.
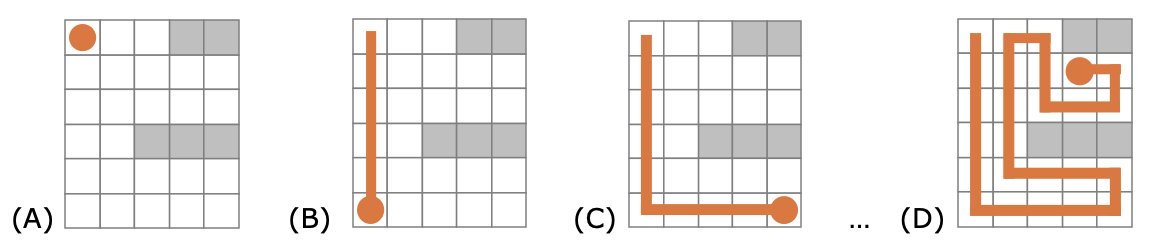
Het doel van het spel is om alle vakjes van het bord te vullen met de slang. Hieronder zie je een voorbeeld. Het hoofd van de slang begint (fig. A) linksboven op positie (0, 0), beweegt dan naar onder (B), dan naar rechts (C), etc. Helemaal rechts (fig. D) zie je een traject dat het hele bord vult. Dit komt overeen met de bewegingen [DOWN, RIGHT, UP, LEFT, UP, RIGHT, DOWN, RIGHT, UP, LEFT].
Ontwerp een backtracking-algoritme om, met zo weinig mogelijk bewegingen, het hele bord te vullen. Je geeft de oplossing terug als een lijst van bewegingen (Directions). Indien er geen oplossing is, geef je null terug. Je moet een solve-methode schrijven die opgeroepen wordt zoals getoond in de gegeven main-methode. In de solve-methode mag je gebruik maken van zelfgeschreven hulpmethodes.
Je krijgt alvast de interface van een Board-klasse om het bord van SnakeFill voor te stellen. Je mag ervan uitgaan dat er hiervan een implementatie beschikbaar is die correct werkt; je moet deze dus niet zelf schrijven. Er zijn ook hulpklassen gegeven om posities en richtingen voor te stellen. In principe volstaan de gegeven methodes in deze klassen om het probleem op te lossen. Je mag elk van deze klassen echter verder uitbreiden met extra methodes die je nuttig acht. Schrijf daarvoor de methode-hoofding en een beschrijving van wat de methode moet doen. Je hoeft de methode zelf niet te implementeren.
public interface Board {
/* Huidige positie van het hoofd van de slang */
Position getCurrentHead();
/* Maakt de gegeven positie deel uit van het bord? */
boolean isValid(Position pos);
/* Is de gegeven positie vrij (geen muur, geen slang)” */
boolean isFree(Position pos);
/* Zijn alle posities van het bord gevuld? */
boolean isFull();
/* Telt het aantal opeenvolgende vrije cellen in de gegeven
richting vanaf het hoofd van de slang.
In situatie (A) in het voorbeeld geeft deze methode
5 terug voor DOWN, 2 voor RIGHT, en 0 voor LEFT en UP. */
int freeCells(Direction dir);
/* Maak de slang n vakken langer in de gegeven richting.
In het voorbeeld ga je van (A) naar (B) met n=5 en dir=DOWN */
void extendSnake(int n, Direction dir);
/* Maak de slang n vakken korter in de gegeven richting.
In het voorbeeld ga je van (B) naar (A) met n=5 en dir=UP */
void retractSnake(int n, Direction dir);
/* Maak een kopie van het bord */
Board copy();
}
/* Positie op het bord */
record Position(int row, int col) {
/* Positie op n vakken vanaf de huidige positie in de
gegeven richting. */
public Position go(Direction dir, int n) {
return switch(dir) {
case RIGHT -> new Position(row, col + n);
case LEFT -> new Position(row, col - n);
case UP -> new Position(row - n, col);
case DOWN -> new Position(row + n, col);
};
}
}
/* Een richting (UP, DOWN, LEFT, RIGHT). */
enum Direction {
UP, DOWN, LEFT, RIGHT;
public static final Direction[] ALL_DIRECTIONS =
{UP, DOWN, LEFT, RIGHT};
…
/* Geef de omgekeerde richting terug
(UP <-> DOWN, LEFT <-> RIGHT) */
public Direction opposite() { … };
}
public static void main(String[] args) {
var board = … /* Maak een bord (dit hoef je niet te schrijven) */
var solution = solve(board);
if (solution != null)
System.out.println(solution);
else
System.out.println("No solution");
}
public static List<Direction> solve(Board board) {
// TODO
}